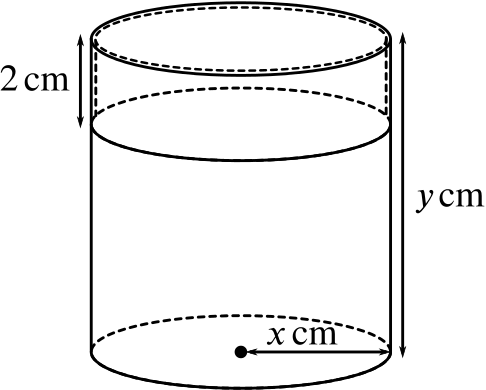
A cylindrical tin and its tight-fitting cylindrical lid (overlapping the tin by \(\quantity{2}{cm}\)) are to be made from thin sheet metal. When made, the total area of sheet metal used is \(\quantity{350\pi}{cm^2}\). The base radius of the tin is \(\quantity{x}{cm}\) and its height is \(\quantity{y}{cm}\) as shown in the diagram. Show that, neglecting the thickness of the metal, \[x^2+xy+2x=175.\]
Deduce that the volume, \(\quantity{V}{cm^3}\), of the tin is given by \[V= \pi(175x-2x^2-x^3).\]
The volume of the tin is \[V= \pi x^2 y.\]
We can eliminate \(y\) by rearranging equation \(\eqref{eq:1}\) to find that \(xy=175-x^2-2x\), and so \[V=\pi x^2 y=\pi x(xy)=\pi x(175-x^2-2x)=\pi(175x-x^3-2x^2).\]
If \(x\) may vary, find the values of \(x\) and \(y\) for which \(V\) has its maximum value.
We differentiate \(V\) with respect to \(x\), giving \[\frac{dV}{dx}=\pi(175-3x^2-4x)=0,\] so to find stationary points of \(V\), we must solve \[3x^2+4x-175=0.\]
We can factorise this equation as \((3x+25)(x-7)=0\) (or use the quadratic formula).
Since \(x\) is the radius of the tin, it must be positive, so \(x=7\).
We have that \[\frac{d^2V}{dx^2}=\pi(-6x-4),\] which is negative when \(x\) is positive, so \(x=7\) gives a local maximum for \(V\).
Furthermore, as there are no other stationary points for \(V\) with \(x>0\), this must give the maximum possible value for \(V\) for \(x\ge0\).
We need to find the corresponding \(y.\) We saw in the previous part that \[xy=175-x^2-2x,\] so that \[7y=175-49-14=112,\] and hence \(y=16\).

