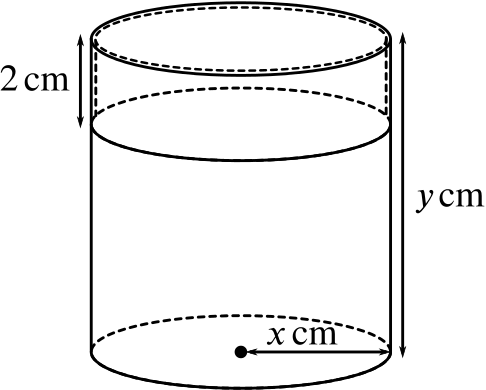
A cylindrical tin and its tight-fitting cylindrical lid (overlapping the tin by \(\quantity{2}{cm}\)) are to be made from thin sheet metal. When made, the total area of sheet metal used is \(\quantity{350\pi}{cm^2}\). The base radius of the tin is \(\quantity{x}{cm}\) and its height is \(\quantity{y}{cm}\) as shown in the diagram. Show that, neglecting the thickness of the metal, \[x^2+xy+2x=175.\]
Deduce that the volume, \(\quantity{V}{cm^3}\), of the tin is given by \[V= \pi(175x-2x^2-x^3).\]
If \(x\) may vary, find the values of \(x\) and \(y\) for which \(V\) has its maximum value.
Can you work out the surface area and volume of this tin and lid in terms of \(x\) and \(y\)? Now can you eliminate \(y\)?

