What's the area between $f_k(x) = x(x-k)(x-2)$ and the $x$-axis?

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

Let \(0< k <2\). Below is sketched a graph of \(y=f_k(x)\) where \(f_k(x) = x(x-k)(x-2)\). Let \(A(k)\) denote the area of the shaded region.

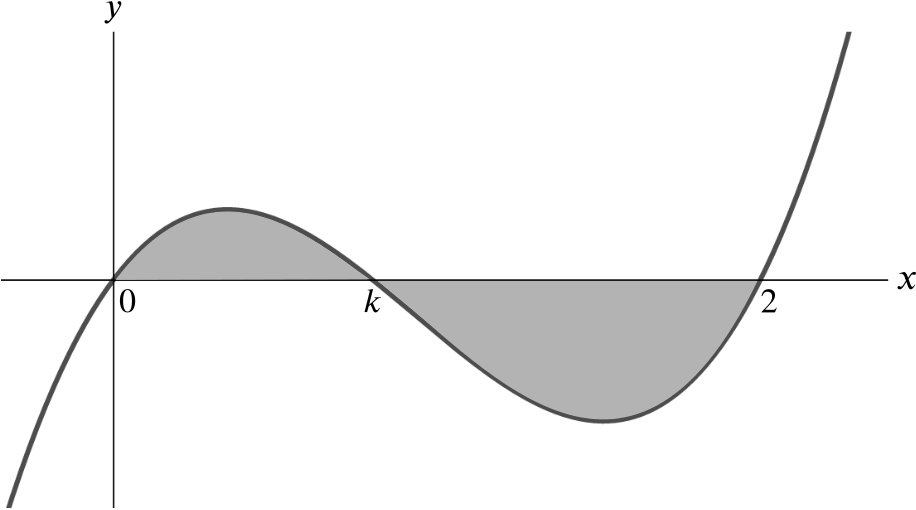
1. Without evaluating them, write down an expression for \(A(k)\) in terms of two integrals.

2. Explain why \(A(k)\) is a polynomial in \(k\) of degree \(4\) or less. [You are not required to calculate \(A(k)\) explicitly.]

3. Verify that \(f_k (1+t) = -f_{2-k}(1-t)\) for any \(t\).

4. How can the graph of \(y=f_k(x)\) be transformed to the graph of \(y = f_{2-k}(x)\)?

   Deduce that \(A(k)=A(2-k)\).

5. Explain why there are constants \(a, b, c\) such that \[A(k) = a(k-1)^4 + b(k-1)^2 + c.\] [You are not required to calculate \(a,b, c\) explicitly.]