Let \(0< k <2\). Below is sketched a graph of \(y=f_k(x)\) where \(f_k(x) = x(x-k)(x-2)\). Let \(A(k)\) denote the area of the shaded region.
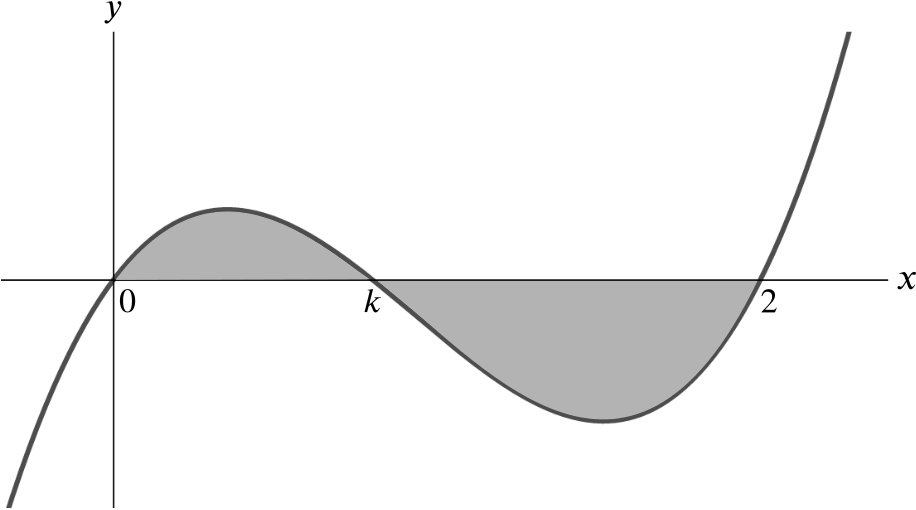
- Without evaluating them, write down an expression for \(A(k)\) in terms of two integrals.
We need to consider the two shaded regions separately, because one is above the \(x\)-axis (giving a positive area), and one is below the \(x\)-axis (giving a negative area), so we can’t just take the integral \(\displaystyle\int_0^2 \! f_k(x) \, \mathrm{d}x\).
Instead, we have
\[A(k) = \displaystyle\int_0^k \! f_k(x) \, \mathrm{d}x - \displaystyle\int_k^2 \! f_k(x) \, \mathrm{d}x,\]
as the negative sign in front of the second integral cancels out the negative sign of the area between \(x=k\) and \(x=2\).
Therefore,
\[A(k) = \displaystyle\int_0^k \! x(x-k)(x-2) \, \mathrm{d}x - \displaystyle\int_k^2 \! x(x-k)(x-2) \, \mathrm{d}x.\]
- Explain why \(A(k)\) is a polynomial in \(k\) of degree \(4\) or less. [You are not required to calculate \(A(k)\) explicitly.]
\(A(k)\) is certainly a polynomial in \(k\). Could it include a \(k^5\) term?
Only if you have an \(x^5\) term or a \(kx^4\) term after integrating, which means having an \(x^4\) term or a \(kx^3\) term before integrating.
Neither is possible, by looking at \(x(x-k)(x-2)\), and the same argument works for powers of \(k\) higher than \(5\).
Hence \(A(k)\) is a polynomial in \(k\) of degree at most \(4\).
- Verify that \(f_k (1+t) = -f_{2-k}(1-t)\) for any \(t\).
Let’s start by thinking about what \(f_k(1+t)\) and \(f_{2-k}(1-t)\) are, given that \(f_{k}(x)=x(x-k)(x-2)\).
To find \(f_{k}(1+t)\), we need to substitute \(1+t\) for \(x\) in the formula for \(f_{k}(x).\) This gives us \[f_k(1+t) = (1+t)(1+t-k)(1+t-2).\]
To find \(f_{2-k}(1-t)\), we need to substitute \(1-t\) for \(x\), but we also need to substitute \(2-k\) for \(k.\) Therefore \[f_{2-k}(1-t) = (1-t)(1-t-(2-k))(1-t-2).\]
If we think about what we are aiming for, we can see that the first two brackets involve \(1+t\), which is a good sign. It would be helpful to rewrite the last bracket in a way that also involves \(1+t.\) We can write \(t-1\) as \(1+t-2\) which means that
\[\begin{align*} -f_{2-k}(1-t) \hspace{2mm} & =(1+t)(1+t-k)(1+t-2) \\ & = f_{k}(1+t) \quad \text{as required.}\\ \end{align*}\]We started from the RHS because it looks messier and we wanted to get it to a simpler expression. We could have started with the LHS.
- How can the graph of \(y=f_k(x)\) be transformed to the graph of \(y = f_{2-k}(x)\)?
From part (iii), we have that
\[f_k(1+t) = -f_{2-k}(1-t).\]
If we substitute \(t\) with \(1-x\), the above equation becomes equivalent to
\[-f_k(2-x) =f_{2-k}(x).\]
Now, \(f_k(2-x)\) is the reflection of \(f_k(x)\) in the line \(x=1\).
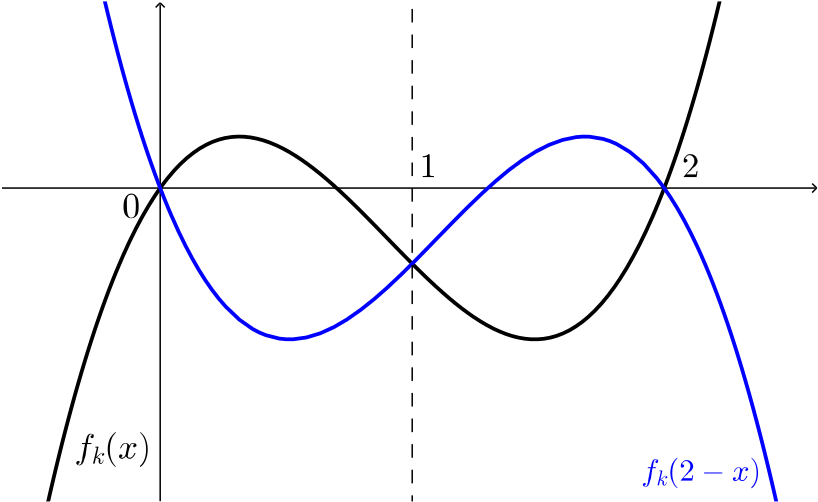
A second transformation is now required because of the minus sign in front of \(f_{k}\). This is a reflection in the \(x\)-axis.
Together these transformations are the same as a rotation \(180^{\circ}\) around the point \((1,0)\).
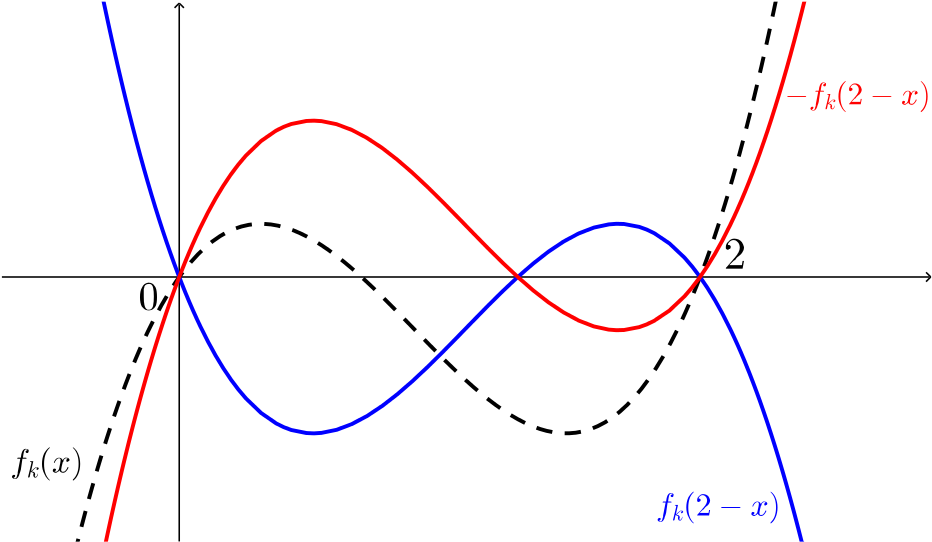
In fact, combining two reflections always gives you a rotation about the point where the two mirror lines intersect.
Deduce that \(A(k)=A(2-k)\).
As we can see in the sketch above, since we’re rotating \(180^\circ\) around a point on the x axis, the area between the graph and the \(x\)-axis remains the same for \(f_k\) and \(f_{2-k}\), i.e. \(A(k) = A(2-k)\).
Or else we could say that since both of the reflections preserve the shaded area, combining them does too.
- Explain why there are constants \(a, b, c\) such that \[A(k) = a(k-1)^4 + b(k-1)^2 + c.\] [You are not required to calculate \(a,b, c\) explicitly.]
We know that \(A(k) = A(2-k)\), so \(A(1-k) = A(2-(1-k)) = A(1+k)\), and so \(y = A(k)\) is symmetrical about the line \(k = 1\).
So if we translate \(y = A(k)\) by \(1\) to the left, then it is even, so if we express \(A(k)\) as powers of \((x-1)\), only even powers are possible.
Therefore we have \(A(k) = a(k-1)^4 + b(k-1)^2 + c\) for some constants \(a, b, c\).

