What can we say if $y = m(x-a)$ is tangent to $y = x^3 - x$?

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

The graphs of \(y = x^3 - x\) and \(y = m(x-a)\) are drawn on the axes below. Here \(m>0\) and \(a \le -1\).

The line \(y=m(x-a)\) meets the \(x\)-axis at \(A = (a,0)\), touches the cubic \(y=x^3 -x\) at \(B\) and intersects again with the cubic at \(C\). The \(x\)-coordinates of \(B\) and \(C\) are respectively \(b\) and \(c\).

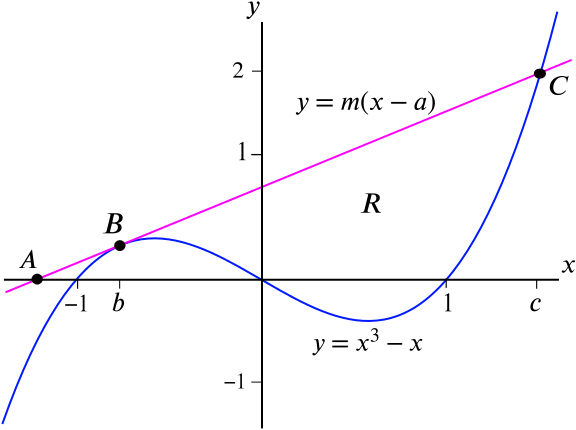
1. Use the fact that the line and cubic touch when \(x=b\), to show that \(m=3b^2-1\).

2. Show further that \[a = \frac{2b^3}{3b^2 - 1}.\]

3. If \(a=-10^6\), what is the approximate value of \(b\)?

4. Using the fact that \[x^3 - x - m(x-a) = (x-b)^2 (x-c)\] (which you need not prove), show that \(c=-2b\).

5. \(R\) is the finite region bounded above by the line \(y=m(x-a)\) and bounded below by the cubic \(y = x^3 - x\). For what value of \(a\) is the area of \(R\) largest?

   Show that the largest possible area of \(R\) is \(\dfrac{27}{4}\).