The graphs of \(y = x^3 - x\) and \(y = m(x-a)\) are drawn on the axes below. Here \(m>0\) and \(a \le -1\).
The line \(y=m(x-a)\) meets the \(x\)-axis at \(A = (a,0)\), touches the cubic \(y=x^3 -x\) at \(B\) and intersects again with the cubic at \(C\). The \(x\)-coordinates of \(B\) and \(C\) are respectively \(b\) and \(c\).
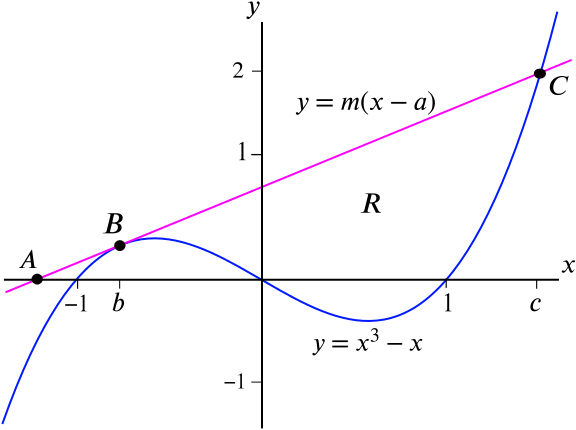
- Use the fact that the line and cubic touch when \(x=b\), to show that \(m=3b^2-1\).
For the line and the cubic to touch at \(x=b\), the gradients must be equal at this point.
The gradient of the cubic is given by \[\frac{dy}{dx} = 3x^2 - 1,\] and the gradient of the line is \(m\).
Therefore, equating these expressions at \(x=b\) gives \[m = 3b^2 - 1.\]
- Show further that \[a = \frac{2b^3}{3b^2 - 1}.\]
The value of \(y\) must be the same for each graph at \(x=b\). Hence we have \[b^3 - b = m(b-a).\]
Now from part (i) we know that \(m=3b^2 - 1\), so substituting this into the above expression gives \[b^3 - b = (3b^2 - 1)(b-a).\]
We can rearrange this to get \(a\) by dividing by \(3b^2-1\) to give \[b-a=\frac{b^3 - b}{3b^2 - 1}\] and then finding \[\begin{align*} a &{}= b - \frac{b^3 - b}{3b^2 - 1}\\ &{}= \frac{b(3b^2-1) -(b^3 - b)}{3b^2 -1}\\ &{}= \frac{2b^3}{3b^2 - 1}. \end{align*}\]- If \(a=-10^6\), what is the approximate value of \(b\)?
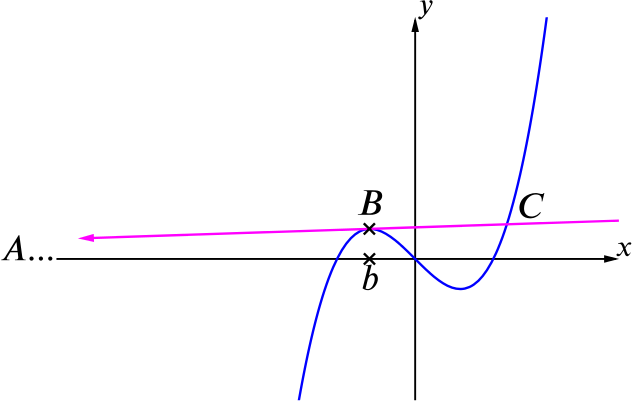
If \(a\) is large and negative, the line \(y=m(x-a)\) (which is still a tangent to the curve somewhere between \(-1\) and \(0\)) will be almost horizontal.
So the point \(B\) will lie almost at the maximum point of the curve, which is where \(3x^2-1=0\), so \(b\approx-\dfrac{1}{\sqrt{3}}\).
Another way of thinking about this is that the fraction in (ii) must be very large and negative.
For this, either \(b\) must be very large and negative, or the denominator must be very close to zero.
But \(b\) lies between \(-1\) and \(0\), so it must be the latter, and \(3b^2-1\approx0\), giving \(b \approx - \dfrac{1}{\sqrt{3}}\) (taking the negative square root).
- Using the fact that \[x^3 - x - m(x-a) = (x-b)^2 (x-c)\] (which you need not prove), show that \(c=-2b\).
We can put both sides in a polynomial form, so that we can see the coefficients of \(x^3\), \(x^2\) etc. on each side. Doing this gives \[x^3-(m+1)x +ma = x^3 -(2b + c)x^2 +(b^2 + 2bc)x -b^2 c.\]
Since the statement is true for all \(x\), it must be true that the coefficient of any power of \(x\) must be the same on both sides.
In particular the coefficient of \(x^2\) on the left side, \(0\), must be equal to the coefficient on the right side, \(-(2b + c)\). Therefore \(2b+c=0\), and hence \(c=-2b\).
- \(R\) is the finite region bounded above by the line \(y=m(x-a)\) and bounded below by the cubic \(y = x^3 - x\). For what value of \(a\) is the area of \(R\) largest?
Show that the largest possible area of \(R\) is \(\dfrac{27}{4}\).
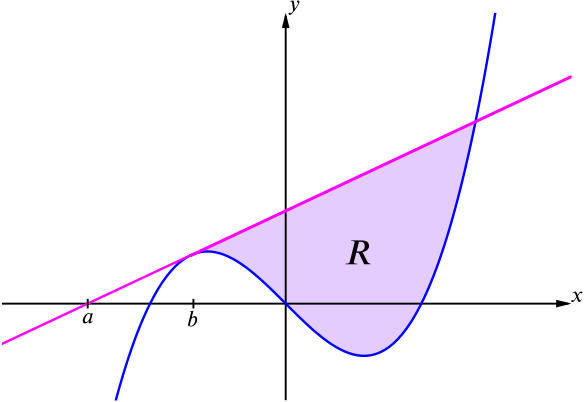
If \(a\) increases (getting closer to \(-1\)), then \(b\) decreases and the line \(y=m(x-a)\) rises, making the area of \(R\) larger.
Therefore we want to choose the largest possible value of \(a\) in order to make the area the largest. So as \(a \le -1\), the area of \(R\) is largest when \(a=-1\).
And when \(a=-1\), the line \(y=m(x-a)\) must be tangent to the curve at the point \((-1,0)\) since this is a point on both the line and the curve for this value of \(a\).
So \(B\) coincides with \(A\) and \(b=-1\).
We can also deduce this algebraically using the earlier results, as follows. By part (ii), we see that \[-1 = \frac{2b^3}{3b^2 - 1}.\]
Rearranging this gives \(2b^3 + 3b^2 - 1 = 0\), which can be factorised as \((b+1)^2 (2b-1) = 0\). Since \(b\) can’t be positive, we conclude that \(b=-1\).
Then using part (iv), we obtain \(c=2\), and from part (i), we see that \(m=3b^2 - 1 = 2\).
So we can now calculate \[\begin{align*} \text{Area of $R$} &{}= \int_b^c (m(x+1) - (x^3 - x)) \, dx \\ &{}= \int_{-1}^2 -x^3 + 3x + 2 \, dx \\ &{}= \left[ -\frac{x^4}{4} + \frac{3x^2}{2} + 2x \right]_{-1}^2 \\ &{}= 6-\left(-\frac{3}{4}\right)\\ &{}= \frac{27}{4}. \end{align*}\]
