The equation in \(x\), \[3x^4 - 16x^3 +18x^2 + k = 0\] has four real solutions
when \(-27 < k < 5\);
when \(5< k <27\);
when \(-27< k <-5\);
when \(-5< k <0\).
The understanding here is that the solutions are distinct.
The number of distinct solutions to \(f(x)=3x^4 - 16x^3 +18x^2 + k = 0\) equals the number of times the graph \(y=f(x)\) crosses the \(x\)-axis, so it’ll be helpful to sketch the graph of \(y = f(x)\).
We can use differentiation to learn about the stationary points and therefore the shape of this graph. So we write \[y=3x^4-16x^3+18x^2+k,\] and then we differentiate to find \[\begin{align*} y' &= 12x^3-48x^2+36x \\ &= 12x(x^2 - 4x + 3) \\ &= 12x(x-3)(x-1). \end{align*}\]To find the stationary points, we solve \(y'= 0\). We see that the stationary points of the graph occur at \(x=0\), \(x=1\) and \(x=3\).
To classify these stationary points, we can use the second derivative. We have \[\begin{align*} y'' &= 36x^2-96x+36 \\ &= 12(3x^2-8x+3). \end{align*}\] Substituting, \[\begin{align*} y''(0) &= 36 > 0, \\ y''(1) &= -24 < 0, \\ y''(3) &= 72 > 0, \end{align*}\]so we find that the stationary points at \(x=0\) and \(x=3\) are minima, and the stationary point at \(x=1\) is a maximum.
If we now substitute \(x=0\), \(1\) and \(3\) into the equation, we find that the coordinates of our minima are \((0,k)\) and \((3,k-27)\), and the coordinates of the maximum are \((1,k+5)\).
Or alternatively, we can say we know the rough shape of the curve (see below) so we know which turning points are maxima, and which are minima.
This information about the curve is summarised in the sketch of \(y=f(x)\) given below.
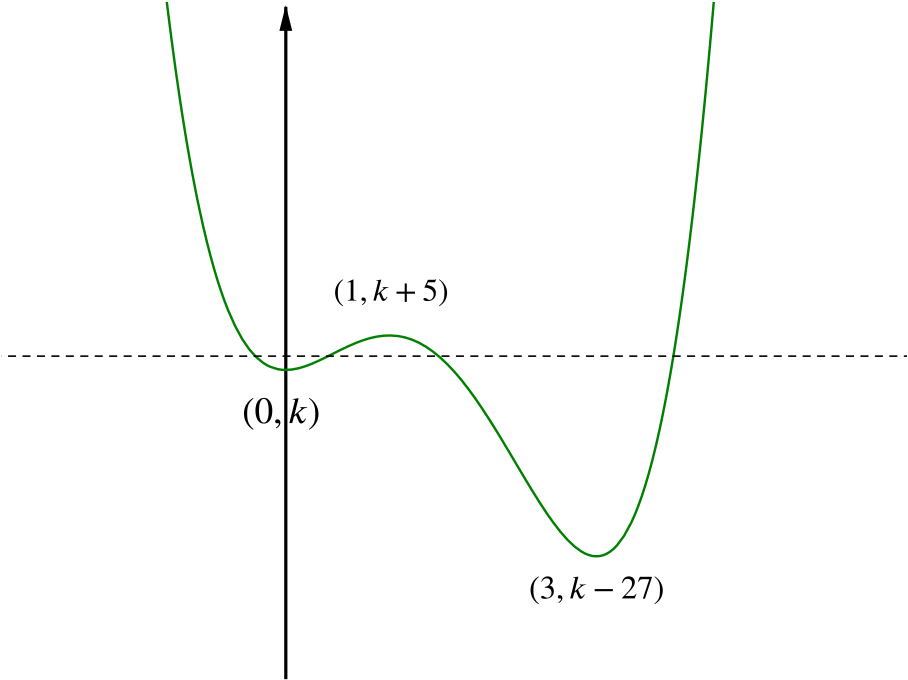
The equation has four real solutions when the graph crosses the \(x\)-axis four times.
This occurs when the \(x\)-axis is in the position of the dotted line in the diagram above.
That is, it’s in a position such that the minima at \((0,k)\) and \((3,k-27)\) are below it, and the maximum at \((1,k+5)\) is above it.
In terms of inequalities, this is when \(k < 0\), \(k-27 < 0\) and \(k+5 > 0\).
So combining these, our final inequality is \(-5 < k < 0\), so the answer is (d).

