Our journey is along a straight line (to think about why see Speed vs velocity). To describe the journey consistently, let us imagine a line with an origin that represents a displacement of zero and let us define the positive direction as being to the right.

If, at time \(t = 0\), the velocity and displacement are zero, can you describe, draw or imagine what the journey is like?
Which direction are you travelling in? Are you speeding up or slowing down?
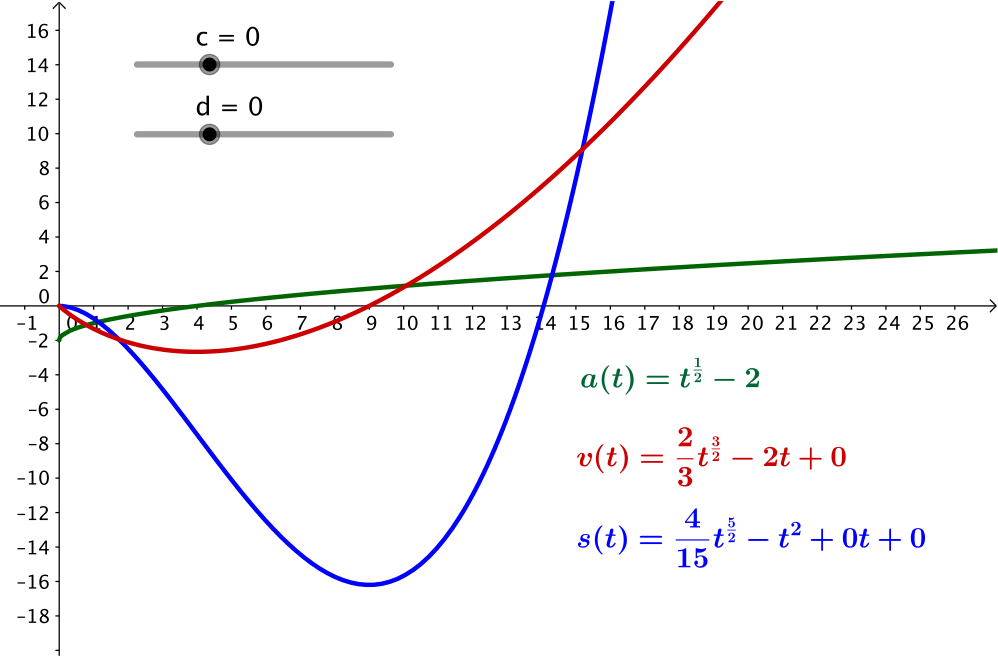
If velocity and displacement are zero at time \(t = 0\), this implies that \(c\) and \(d\) are zero, so we can think of the origin as our starting point.
The times when something about the journey changes are \(t = 4\), \(t= 9\), and \(t = 14\). Can you see why from the graph?
From \(t = 0\) to \(4\)
The object starts from rest and travels left, up to a speed of approximately \(3\).
The velocity is negative (to the left) but decreasing, so it means the magnitude (or speed) is actually getting larger.
From \(t = 4\) to \(9\)
The object is still going left, but the speed is now decreasing, What happens to the object at \(t = 9\)?
From \(t = 9\) to \(14\)
The object is travelling to the right, and the velocity (and speed) is increasing from \(0\). It passes the origin at \(t=14\).
Think about how changes in the journey are represented on the different graphs. For example, when the acceleration is zero, what key features do the different graphs exhibit?
Approximately, for what value of \(c\) is there no negative velocity?
What feature of the journey changes when there is no negative velocity?
What feature of the displacement graph changes when there is no negative velocity?
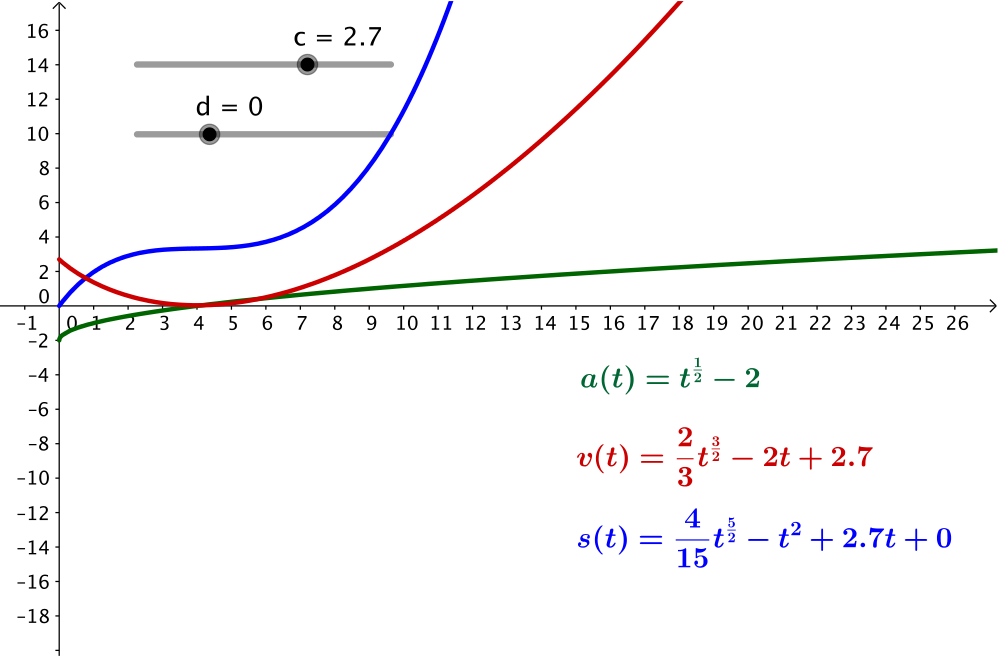
At \(c \approx 2.7\), the velocity graph no longer crosses the \(x\)-axis.
There is now no negative velocity, so the object will always be moving to the right.
If the object is always moving to the right, then the displacement is always increasing. The local maxima and minima of the displacement graph disappear so the displacement function is now an increasing function. Why? What impact does the velocity have on the displacement graph?
The acceleration function is negative for the first \(4\) seconds. What does this mean is happening to the object when
- \(c = 0\)?
- \(c = 3\)?
- \(c = 2\)?
When \(c =0\)
We often think about negative acceleration meaning deceleration or slowing down. But if we remember how we described the journey in the first part of the question, we said ‘The object starts from rest and travels left, up to a speed of approximately \(3\)’.
What is happening here?
If the acceleration is negative the velocity is decreasing. Of course, if the velocity is negative and decreasing, its magnitude is increasing, meaning you are travelling faster. So here, the negative acceleration means travelling to the left and speeding up.
When \(c = 3\)
This is similar to the question above. Velocity is no longer negative, so our acceleration behaves as we would normally think. During the first \(4\) seconds, the object is slowing down while travelling to the right.
When \(c = 2\)
This is a combination of the two cases above. Initially the object slows down as it travels right, but as the velocity reaches zero, the object changes direction, and it starts to speed up as it travels towards the left. At \(t = 4\), it starts to slow down again. (From this point the acceleration is positive, meaning the object is slowing down as it travels left.)
- Now let’s think about \(c=0\) and \(d=2\). How would you describe the journey, and how does it differ from the journey in question 1?
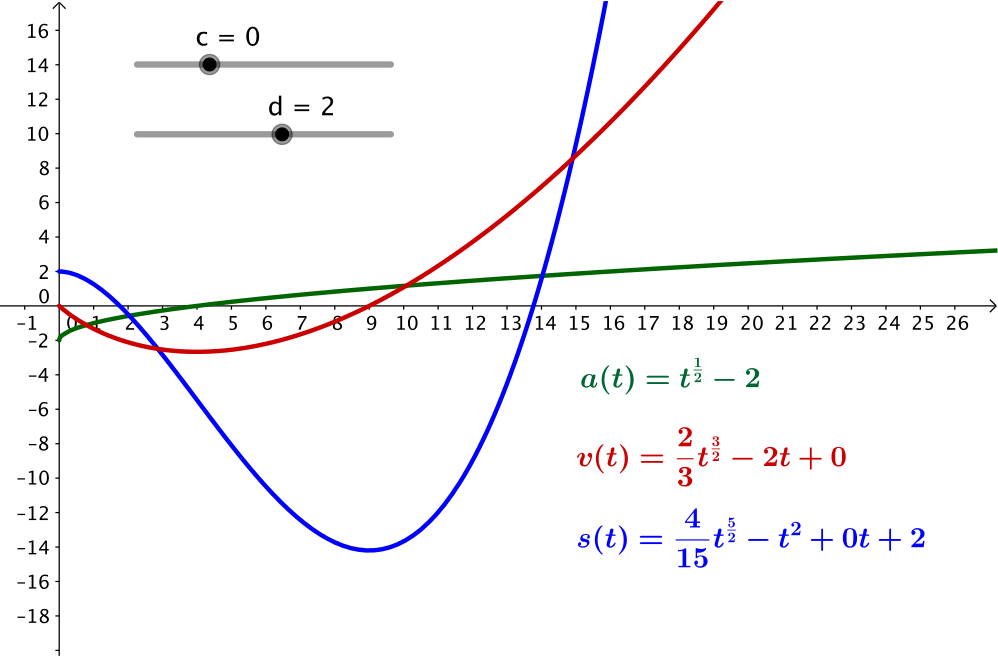
Firstly, changing \(d\) only affects the displacement graph so the velocity and acceleration descriptions from question \(1\) stay the same.
The object now starts \(2\) units to the right of the origin. There are two ways we could think about this. Either the object has changed its starting point by \(2\) units or the origin has moved \(2\) units to the left.
Does that second description seem strange? Remember, we can choose the point from which we want to measure displacement as long as we state what this point is. Often, questions will inform us that displacement equals zero at \(t = 0\). Why do you think this is so common?
Moving our origin is a translation, and we do it to try to make calculations more straightforward. When we think of translations, we might imagine sliding a graph, but we could also imagine sliding the axes, while the graph stays in the same place. This idea of choosing an origin to suit your question can be applied in many areas, and will become more familiar to you as you work with vectors and think about frames of reference.

