If $x^2+y^2\leq1$, when does $x+y$ have a maximum?

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

Let \(Q\) denote the quarter-disc of points \((x,y)\) such that \(x\geq 0\), \(y\geq 0\) and \(x^2+y^2\leq1\) as drawn in Figures A and B below.

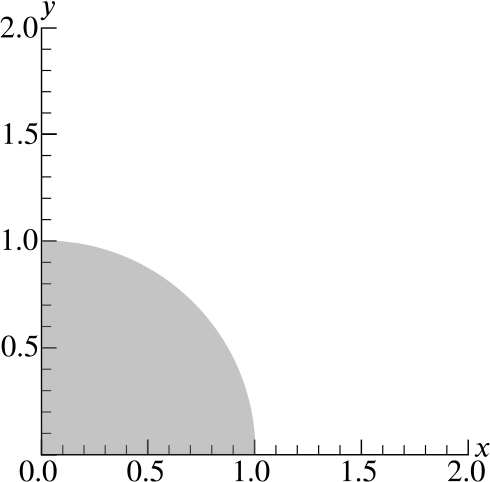
1. On the axes in Figure A, sketch the graphs of \[x+y=\frac{1}{2}, \qquad x+y=1, \qquad x+y=\frac{3}{2}.\]

   What is the largest value of \(x+y\) achieved at points \((x,y)\) in \(Q\)? Justify your answer.

2. On the axes in Figure B, sketch the graphs of \[xy=\frac{1}{4}, \qquad xy=1, \qquad xy=2.\]

   What is the largest value of \(x^2+y^2+4xy\) achieved at points \((x,y)\) in \(Q\)? What is the largest value of \(x^2+y^2-6xy\) achieved at points \((x,y)\) in \(Q\)?

3. Describe the curve \[x^2+y^2-4x-2y=k\] where \(k>-5\).

   What is the smallest value of \(x^2+y^2-4x-2y\) achieved at points \((x,y)\) in \(Q\)?