Let \(Q\) denote the quarter-disc of points \((x,y)\) such that \(x\geq 0\), \(y\geq 0\) and \(x^2+y^2\leq1\) as drawn in Figures A and B below.
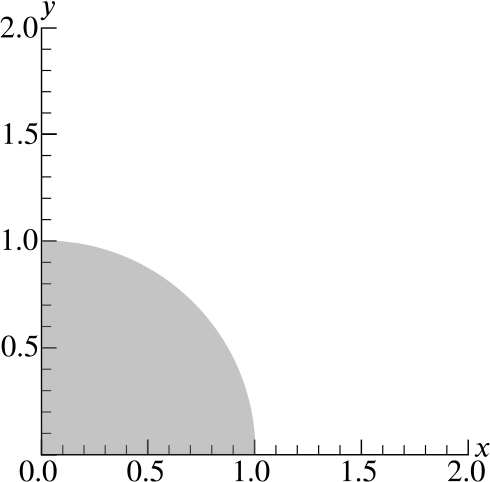

- On the axes in Figure A, sketch the graphs of \[x+y=\frac{1}{2}, \qquad x+y=1, \qquad x+y=\frac{3}{2}.\]
What is the largest value of \(x+y\) achieved at points \((x,y)\) in \(Q\)? Justify your answer.
What do we observe in Figure A after drawing the three graphs? How are they related?
- On the axes in Figure B, sketch the graphs of \[xy=\frac{1}{4}, \qquad xy=1, \qquad xy=2.\] What is the largest value of \(x^2+y^2+4xy\) achieved at points \((x,y)\) in \(Q\)? What is the largest value of \(x^2+y^2-6xy\) achieved at points \((x,y)\) in \(Q\)?
Is this part of the question similar to the previous part in any way?
How could we use the diagram to solve the problem?
‘If the largest values of two functions, say \(f\) and \(g\), are \(\alpha\) and \(\beta\), and \(f+g\) can take the value \(\alpha+\beta\), then the largest value of \(f+g\) is \(\alpha+\beta\).’
Is this logic okay?
What similar statement can we make about the largest value of \(f-g\)?
- Describe the curve \[x^2+y^2-4x-2y=k\] where \(k>-5\). What is the smallest value of \(x^2+y^2-4x-2y\) achieved at points \((x,y)\) in \(Q\)?
How else can we write \(x^2+y^2-4x-2y=k\)? What curve does this look like?

