Let \(Q\) denote the quarter-disc of points \((x,y)\) such that \(x\geq 0\), \(y\geq 0\) and \(x^2+y^2\leq1\) as drawn in Figures A and B below.

- On the axes in Figure A, sketch the graphs of \[x+y=\frac{1}{2}, \qquad x+y=1, \qquad x+y=\frac{3}{2}.\]
What is the largest value of \(x+y\) achieved at points \((x,y)\) in \(Q\)? Justify your answer.
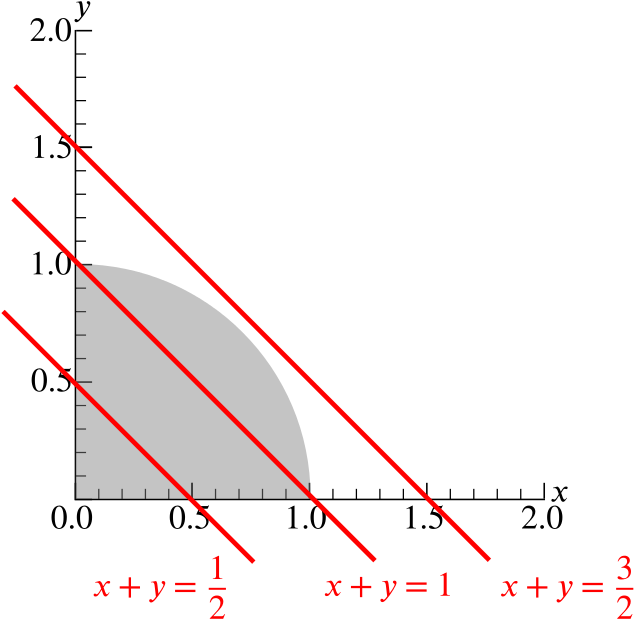
As we can observe, the line \(x+y=k\) will see its largest value for \(k\) when the graph is tangent to \(Q\), that is, when the line is the furthest possible from the origin that still intersects the region.
Hence we want the value of \(k\) such that the pair of simultaneous equations \(x+y=k, x^2+y^2=1\) have a unique solution.
We have \(x^2+(k-x)^2=1\), or \(2x^2-2kx+k^2-1 =0\), which must have a discriminant of zero when viewed as a quadratic in \(x\).
Thus \(4k^2-8(k^2-1)=0\), and so \(k = \sqrt{2}\), and \(x=y=\dfrac{\sqrt2}{2}\). Hence, the largest value of \(x+y\) on \(Q\) is \(\sqrt{2}\).
- On the axes in Figure B, sketch the graphs of \[xy=\frac{1}{4}, \qquad xy=1, \qquad xy=2.\] What is the largest value of \(x^2+y^2+4xy\) achieved at points \((x,y)\) in \(Q\)? What is the largest value of \(x^2+y^2-6xy\) achieved at points \((x,y)\) in \(Q\)?
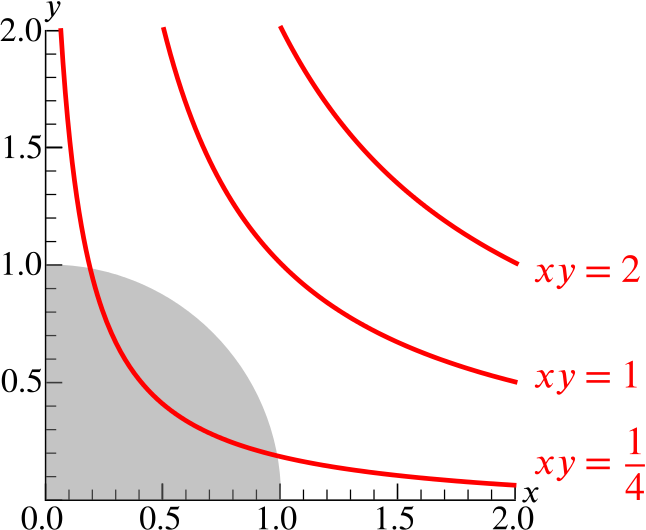
Similarly as above, \(xy\) will achieve its maximum value on \(Q\) when \(x=y=\dfrac{\sqrt2}{2}\), when \(xy\) will be \(\dfrac{1}{2}\).
Since the maximum value of \(x^2+y^2\) in \(Q\) is \(1\), the largest value of \(x^2+y^2+4xy\) on \(Q\) is \(1+4\times \dfrac{1}{2}=3\).
In order to get the largest value of \(x^2+y^2-6xy\) we need the largest value of \(x^2+y^2\), which is \(1\), and the smallest value of \(6xy\), which is \(0\).
So the largest value of \(x^2+y^2-6xy\) on \(Q\) is \(1-0=1\), achieved, for instance, at \(x=1\) and \(y=0\).
- Describe the curve \[x^2+y^2-4x-2y=k\] where \(k>-5\). What is the smallest value of \(x^2+y^2-4x-2y\) achieved at points \((x,y)\) in \(Q\)?
The curve’s equation can be rewritten on completing the square as \[(x^2-4x+4)+(y^2-2y+1)=k+5\] which becomes \[(x-2)^2+(y-1)^2=k+5,\] so it describes a circle of centre \((2,1)\) and radius \(\sqrt{k+5}\). So \(k\) is smaller if \((x,y)\) is closer to \((2,1)\).
In order to find the smallest value of \(x^2+y^2-4x-2y\) achieved at points \((x,y)\) in \(Q\), we should find the closest point to \((2,1)\) in \(Q\).
Since \(Q\) is the quadrant of the disc \(x^2+y^2\le 1\) in the positive quadrant of the plane, and \((2,1)\) is in that same quadrant, the closest point can be obtained by drawing the straight line connecting the points \((0,0)\) and \((2,1)\), and finding where this intersects with the circumference of \(Q\).
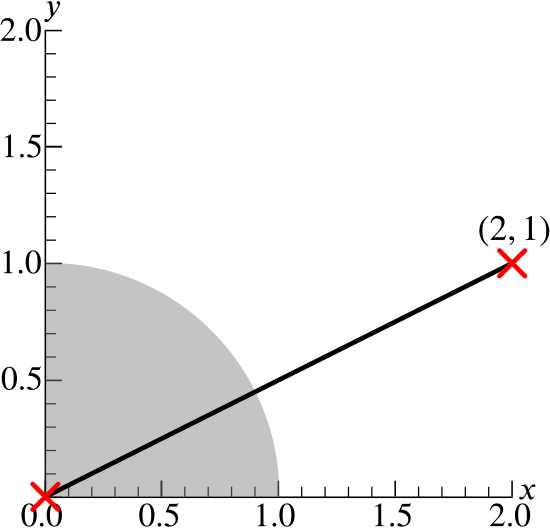
Therefore the result will be the solution of the simultaneous equations \[x-2y=0 \quad\text{and}\quad x^2+y^2=1.\] By substituting \(x=2y\) into the second equation, we get \[5y^2=1\Longrightarrow y=\frac{1}{\sqrt5},\] so \(x = \dfrac{2}{\sqrt5}\). So the smallest value of \(x^2+y^2-4x-2y\) is \[k=1-4\frac{2}{\sqrt5}-2\frac{1}{\sqrt5}=1-\frac{10}{\sqrt5}=1-2\sqrt5,\] where we have substituted for \(x\) and \(y\) into \(x^2+y^2-4x-2y\), noting as a check that \(x^2+y^2=1\).

