Can we show that (circle area)/(triangle area) $\geq \pi$?

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

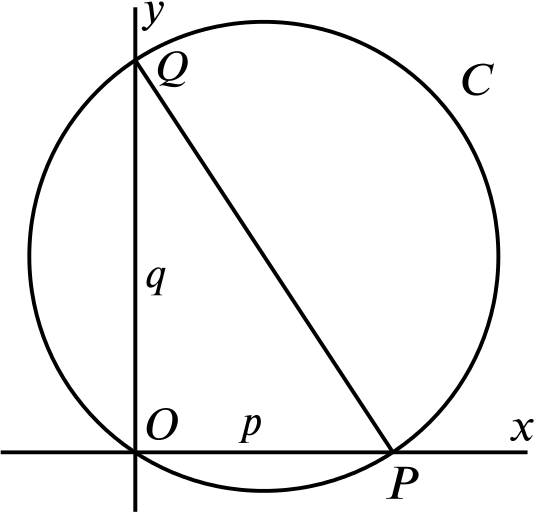
Let \(p\) and \(q\) be positive real numbers. Let \(P\) denote the point \((p,0)\) and \(Q\) denote the point \((0,q)\).

1. Show that the equation of the circle \(C\) which passes through \(P\), \(Q\) and the origin \(O\) is \[x^2 - px + y^2 - qy = 0.\] Find the centre and area of \(C\).

2. Show that \[\frac{\text{area of circle $C$}}{\text{area of triangle $OPQ$}} \ge \pi.\]

3. Find the angles \(OPQ\) and \(OQP\) if \[\frac{\text{area of circle $C$}}{\text{area of triangle $OPQ$}} = 2\pi.\]