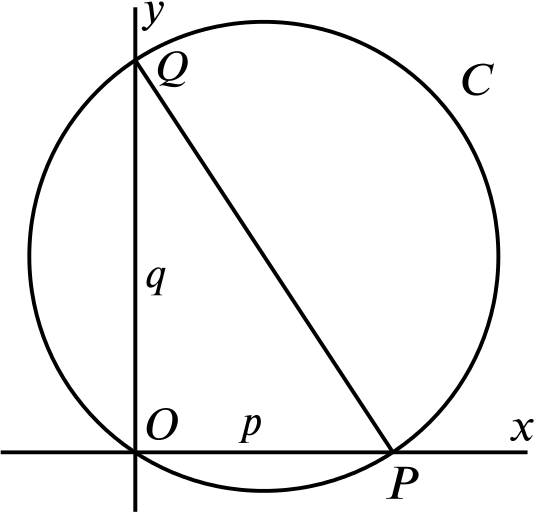
Let \(p\) and \(q\) be positive real numbers. Let \(P\) denote the point \((p,0)\) and \(Q\) denote the point \((0,q)\).
- Show that the equation of the circle \(C\) which passes through \(P\), \(Q\) and the origin \(O\) is \[x^2 - px + y^2 - qy = 0.\]
Substituting in the coordinates \((p,0)\), \((0,q)\) and \((0,0)\), we find that all three points satisfy the equation and so lie on the circle, so we are done.
Alternatively, we can deduce the equation from scratch once we know the centre of the circle.
The line \(PQ\) is a diameter of \(C\), since the angle \(POQ\) is a right-angle, and we know that the angle in a semi-circle is a right-angle.
So the midpoint of \(PQ\), which is \(M \left(\dfrac{p}{2}, \dfrac{q}{2}\right)\), is the centre of the circle. Thus the circle has equation \[\left(x-\frac{p}{2}\right)^2+\left(y-\frac{q}{2}\right)^2=r^2,\] for some \(r\). We can find \(r\) either by substituting the coordinates of a point on \(C\), say \((x,y)=(0,0)\), which gives \(r^2=\left(\dfrac{p}{2}\right)^2+\left(\dfrac{q}{2}\right)^2=\dfrac{p^2+q^2}{4}\), or by finding the radius, which is \(OM=AM=BM\), giving the same result.
Find the centre and area of \(C\).
Just using the given equation, we can complete the square to obtain \[\left(x - \frac{p}{2}\right)^2 + \left(y - \frac{q}{2}\right)^2 -\frac{p^2 + q^2}{4} = 0\] which is the equation of the circle with centre \(\left(\dfrac{p}{2},\dfrac{q}{2}\right)\) and area \(\pi\dfrac{p^2+q^2}{4}\).
Alternatively, using the argument above, we already know the centre of the circle and \(r^2\), and the area is \(\pi r^2=\pi\dfrac{p^2+q^2}{4}\).
- Show that \[\frac{\text{area of circle $C$}}{\text{area of triangle $OPQ$}} \ge \pi.\]
The area of \(OPQ\) is \(\dfrac{1}{2}pq\), so \[\frac{\text{area of circle $C$}}{\text{area of triangle $OPQ$}} = \pi\frac{(p^2+q^2)/4}{pq/2} = \pi\frac{p^2+q^2}{2pq}\]
Then we note that \[\pi\dfrac{p^2 + q^2}{2pq} \ge \pi \iff p^2 + q^2 \ge 2pq \iff (p-q)^2 \ge 0\] which always holds, and so the required inequality is true.
- Find the angles \(OPQ\) and \(OQP\) if \[\frac{\text{area of circle $C$}}{\text{area of triangle $OPQ$}} = 2\pi.\]
From our previous expression we have \[\pi\frac{p^2+q^2}{2pq} = 2\pi \iff p^2 + q^2 = 4pq.\]
Then if we divide through by \(q^2\) (which we know is non-zero), we get \[\left(\frac{p}{q}\right)^2 - 4\left(\frac{p}{q}\right) + 1 = 0\] which is a quadratic in \(\dfrac{p}{q}\) with solution \[\frac{p}{q} = \frac{4 \pm \sqrt{16-4}}{2} = 2 \pm \sqrt{3}.\]
Now since triangle \(OPQ\) is right-angled, we have that \(\dfrac{p}{q} = \tan OQP\) and \(\dfrac{q}{p} = \tan OPQ\).
Then since the solutions are reciprocals of each other, we have \[\{\tan OQP, \tan OPQ\} = \{2 + \sqrt{3}, 2 - \sqrt{3}\},\] where the order depends on which of \(p\) and \(q\) is larger: if \(p>q\), then \(\tan OQP=2+\sqrt{3}\); if \(p<q\), then \(\tan OQP=2-\sqrt{3}\).
Thus \(\{OQP, OPQ\}=\{\arctan(2+\sqrt{3}), \arctan(2-\sqrt{3}\}\) in some order, depending on whether \(p>q\) or \(p<q\).
[Incidentally, it turns out that \(\arctan(2-\sqrt{3})=\dfrac{\pi}{12}\) and \(\arctan(2+\sqrt{3})=5\dfrac{\pi}{12}\), as we will learn at Trigonometry: Compound Angles.]

