I slowly pull a weight along a (rough) table using a piece of string, moving my hand in a straight line.
This applet shows the situation in an ideal setting: the weight is at \(P\), and the end of the string is at \(A\). Move \(A\) to see what happens. (Note that if you move \(A\) backwards again in this applet, the weight simply retraces its path, which is not what would happen in reality.)
You can use the slider (\(a\)) to adjust the length of the string.
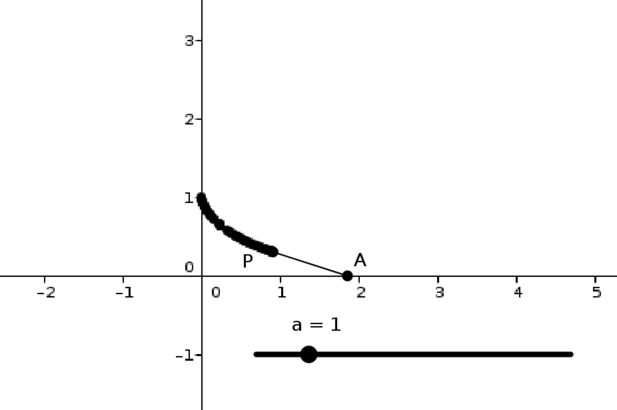
What is the shape of the path that the weight traverses?
As in Approach 1, from the applet or by thinking about the problem, how does the line \(AP\) relate to the path?
It turns out that there is a close relationship between this path, called a tractrix, and a catenary, as shown in this applet:
From the point \(A\), we draw a vertical line to meet the catenary \(y=a\cosh(x/a)\) at \(B\). We draw a tangent to the catenary at \(B\), and drop a perpendicular from \(A\) to meet this tangent at \(Q\).
Move \(A\) to see what happens.
What do you notice as you move the point \(A\)?
How does this help us to find an equation for the tractrix?
You may well find that the answer you get using this approach is different from that obtained from Approach 1. Are they equivalent, or is one of the approaches flawed?

