I slowly pull a weight along a (rough) table using a piece of string, moving my hand in a straight line.
This applet shows the situation in an ideal setting: the weight is at \(P\), and the end of the string is at \(A\). Move \(A\) to see what happens. (Note that if you move \(A\) backwards again in this applet, the weight simply retraces its path, which is not what would happen in reality.)
You can use the slider (\(a\)) to adjust the length of the string.
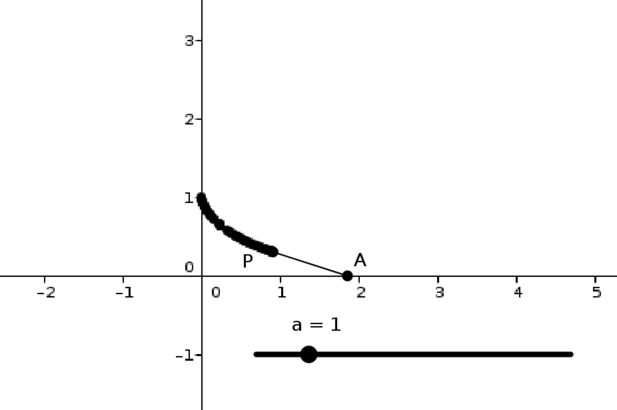
What is the shape of the path that the weight traverses?
As in Approach 1, from the applet or by thinking about the problem, how does the line \(AP\) relate to the path?
As in Approach 1, the line \(AP\) appears to be a tangent to the path.
This is true, since the weight is always being pulled in the direction of the string. As it is moving slowly (due to friction), it will move in the direction it is being pulled.
It turns out that there is a close relationship between this path, called a tractrix, and a catenary, as shown in this applet:
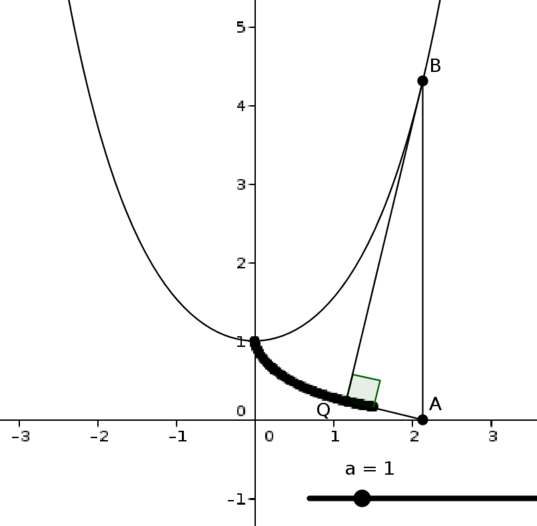
From the point \(A\), we draw a vertical line to meet the catenary \(y=a\cosh(x/a)\) at \(B\). We draw a tangent to the catenary at \(B\), and drop a perpendicular from \(A\) to meet this tangent at \(Q\).
What do you notice as you move the point \(A\)?
How does this help us to find an equation for the tractrix?
It seems that the point \(Q\) traces out a path that looks very similar to a tractrix – we claim that it is, in fact, a tractrix.
We let the \(x\)-coordinate of \(A\) be \(t\), so the coordinates of \(B\) are \((t, a\cosh(t/a))\).
Step 1: The lengths \(AQ\) and \(BQ\)
First of all, we argue that \(AQ=a\). In the diagram below, we have marked the angle the tangent at \(B\) makes with the horizontal as \(\psi\). It follows that \(\tan\psi=\frac{dy}{dx}\).
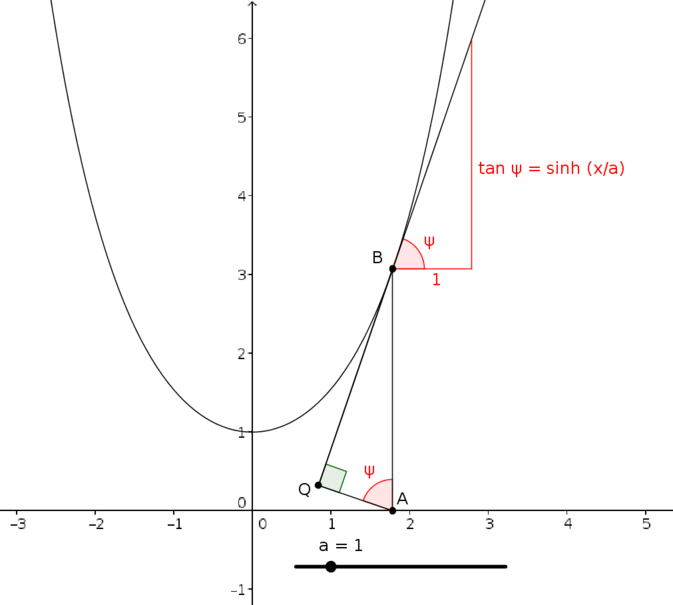
Since \[\frac{dy}{dx}=\sinh\Bigl(\frac{x}{a}\Bigr),\] using the equation of the catenary, it follows that at \(B\), where \(x=t\), \(\tan\psi=\sinh(x/a)\).
We have also drawn a triangle on to illustrate the gradient. We see that the hypotenuse of this triangle has length \(\sqrt{1+\sinh^2(x/a)}=\cosh(x/a)\).
Furthermore, since \(AB\) is vertical, the angle \(\angle BAQ\) is also equal to \(\psi\) (since \(\angle ABQ=90^\circ-\psi\)), so the two triangles shown are similar.
In the triangle \(BAQ\), the hypotenuse length is the \(y\)-coordinate of \(B\), which is \(a\cosh(t/a)\). So by comparing the similar triangles, we see that \(AQ=a\) and \(BQ=a\sinh(t/a)\).
This may well remind us of what we discovered about catenaries in From parabolas to catenaries, namely that they satisfy the equation \(\tan\psi=s/a\), or \[s=a\tan\psi=a\sinh(t/a)=BQ.\] So the length \(BQ\) equals the arc length of the catenary from \((0,a)\) to \(B\).
Step 2: \(BQ\) is normal to the locus of \(Q\)
If we can show this, it will follow that \(AQ\) is tangent to the locus at \(Q\), and thus that the locus of \(Q\) is the tractrix we are after.
The simplest way to think about this may be to imagine a piece of string wrapped around the catenary, with one end attached a long way up and the loose end initially at \((0,a)\).
As the string unwraps, it is held taut, so that the end of the string is at \(Q\). This works, because \(BQ\) is the arc length from \((0,a)\) to \(B\).
As the string unwraps a little more, the end of the string at \(Q\) will approximately describe an arc of a circle, so the radius of this circle, \(BQ\), is perpendicular to the arc traversed by \(Q\). Try it with a piece of string wrapped around an object to get a feeling for what is happening here! (This is a little bit hand-wavey, but it can be made rigorous if desired.)
It follows that \(AQ\) is tangential to the locus of \(Q\), and so \(Q\) describes the tractrix.
Even more, though: we have discovered that \(Q\) is the involute of the catenary. (An involute of a curve is the new curve one gets by unwrapping a piece of string wrapped around it in the way we have described.)
You may well be wondering: how did we know that we should try using a catenary? Mathematicians spent many years studying curves, especially in the 19th century, and determining involutes and the inverse concept called evolutes was one of they things they did with many curves. So this connection would have been discovered through their explorations.
Step 3: Write down an equation for the tractrix
The point \(A\) is at \((t,0)\). The line segment \(AQ\) has length \(a\) and makes an angle of \(\psi\) with the vertical, as the diagram above shows. Therefore the point \(Q\) has parametric coordinates \[\begin{align*} Q(t-a\sin\psi,a\cos\psi)&=\left(t-a\Bigl(\frac{\sinh(t/a)}{\cosh(t/a)}\Bigr), a\Bigl(\frac{1}{\cosh(t/a)}\Bigr)\right)\\ &=\left(t-a\tanh\Bigl(\frac{t}{a}\Bigr), a\sech\Bigl(\frac{t}{a}\Bigr)\right) \end{align*}\]You may well find that the answer you get using this approach is different from that obtained from Approach 1. Are they equivalent, or is one of the approaches flawed?

