Some of the ideas in the Serpentine example can be used to find the area between a curve and the \(x\)-axis. They can also be used to find the area between curves. The result for the area between a curve and the \(x\)-axis, called the trapezium rule, is illustrated below.
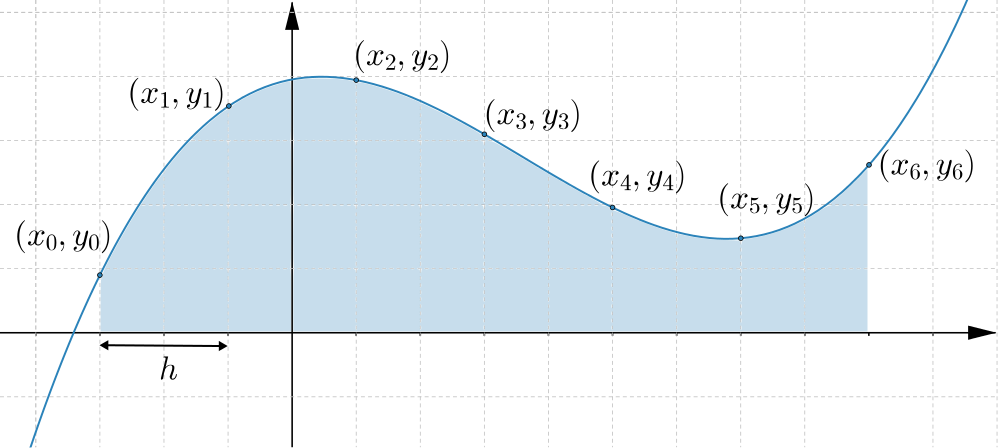
In this graph the points are spread out evenly, so that the \(x\)-coordinates increase by \(h\) each time. By approximating the area under the graph using trapezia, we have \[\text{Area between graph and $x$-axis}\approx \dfrac{h}{2}\Big(y_{0}+2(y_{1}+y_{2}+ y_{3}+y_{4}+y_{5})+y_{6}\Big)\]
What would the formula be if we had \(n+1\) evenly spaced points?
How could the formula be written if we knew we had the graph of a function, \(f(x)\)?

