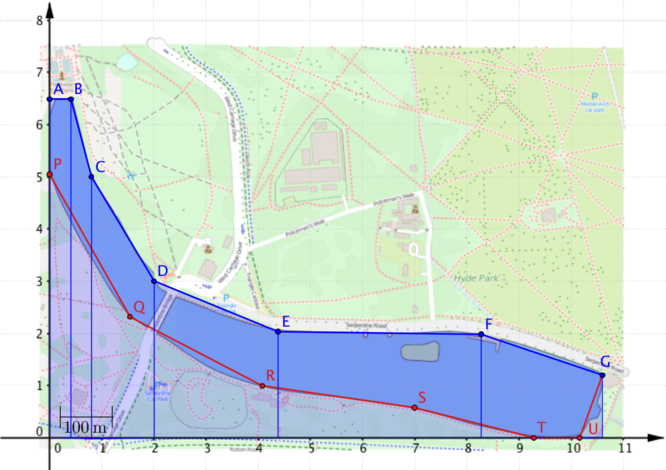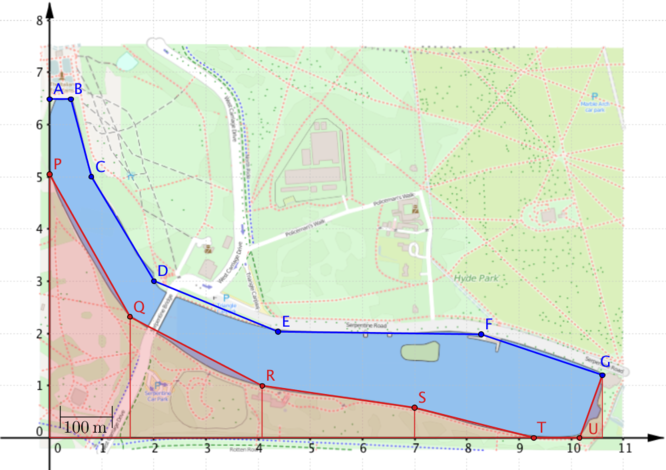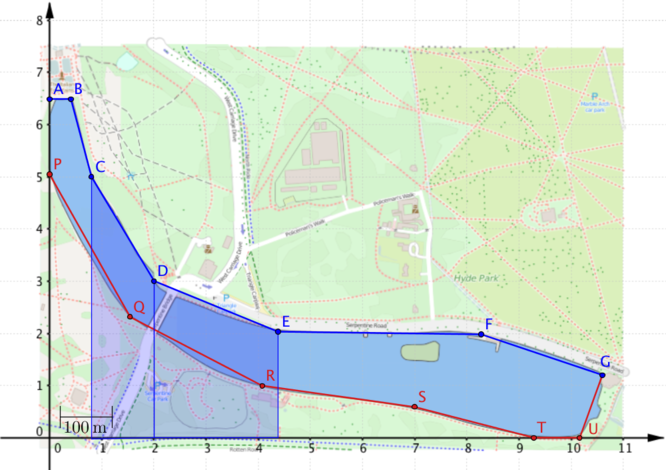
Can you explain why the following equation will give us the area of the region covered by the two trapezia in this diagram?
\[\text{area} = (2.0-0.8) \times \dfrac{5.0+3.0}{2}+ (4.4-2.0)\times \dfrac{3.0+2.0}{2}\]
We can extend this idea to find the area of the entire region between the \(x\)-axis and the top (blue) boundary, formed by joining the points A,B,…,G, and use this to find the area of the lake.
Streamlining the calculations
In the previous calculations we had to work out the area of each trapezium separately, but you may have noticed that the lengths of the parallel sides of most of the trapezia occur twice in the equations. For example, \(3.0\) occurs twice in the equation which gives the blue area. It would be nice to exploit this in some way.
How might the calculations have been different if the points on the boundary had been chosen in this way?
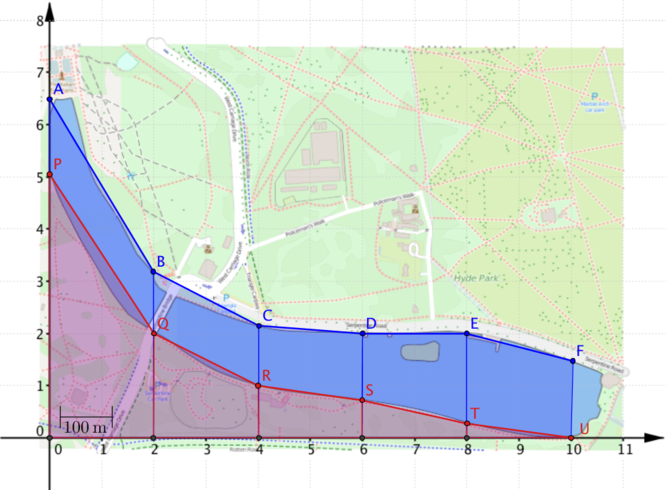
We’ll look in more detail at how the choice of points affects the calculation of the area between the blue boundary and the \(x\)-axis.
\[\begin{align*} \text{blue area}&= 2\left(\dfrac{6.5+3.2}{2}\right)+2\left(\dfrac{3.2+2.1}{2}\right)+2\left(\dfrac{2.1+2.0}{2}\right)\\ & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad+2\left(\dfrac{2.0+2.0}{2}\right)+2\left(\dfrac{2.0+1.5}{2}\right)\\ &=\dfrac{2}{2} \Big( 6.5+3.2+3.2+2.1+2.1+2.0+2.0+2.0+2.0+1.5 \Big)\\ &=\dfrac{2}{2}\Big( 6.5+2(3.2+2.1+2.0+2.0)+1.5\Big) \end{align*}\]You may be wondering why this equation hasn’t been simplified further. If you’re trying to generalise, it can be helpful not to simplify expressions too much before looking at them carefully.
For example, there are lots of terms in these calculations and there are lots of \(2\)s.
Can you explain where each of \(2\)s in the equation comes from?
Which parts of the equation would change if the trapezia were of width 3?
How many trapezia have we used and how many points have we drawn on the lake boundary?
The choice of evenly spaced coordinates allows us to streamline the calculations for finding the blue area and the red areas. In this particular problem we actually want to find the area between the blue and the red boundaries. How could you combine the information from the coordinates of the red and blue points into a single calculation?
The choice of evenly spaced points with the same \(x\)-coordinates means that we can choose between calulating the red and blue areas separately or combining the coordinates into a single calculation.
What could be the advantages or disadvantages of the two approaches?