In this section we have provided some tools to help you explore cubic curves. You should try to get as far as you can with the problem before using the tools. For example,
If you have found examples of cubic curves that satisfy the criteria, can you generalise your examples?
If you haven’t managed to come up with an equation for an example, have you tried to sketch one or more examples of cubic curves that satisfy the criteria?
If you have been able to express the criteria in algebra, have you thought about what else you need to know to find an example that meets these criteria?
Thinking about cubics
If you know \(f(x)\) is a cubic function of \(x\), what can you say algebraically about \(f(x)\)?
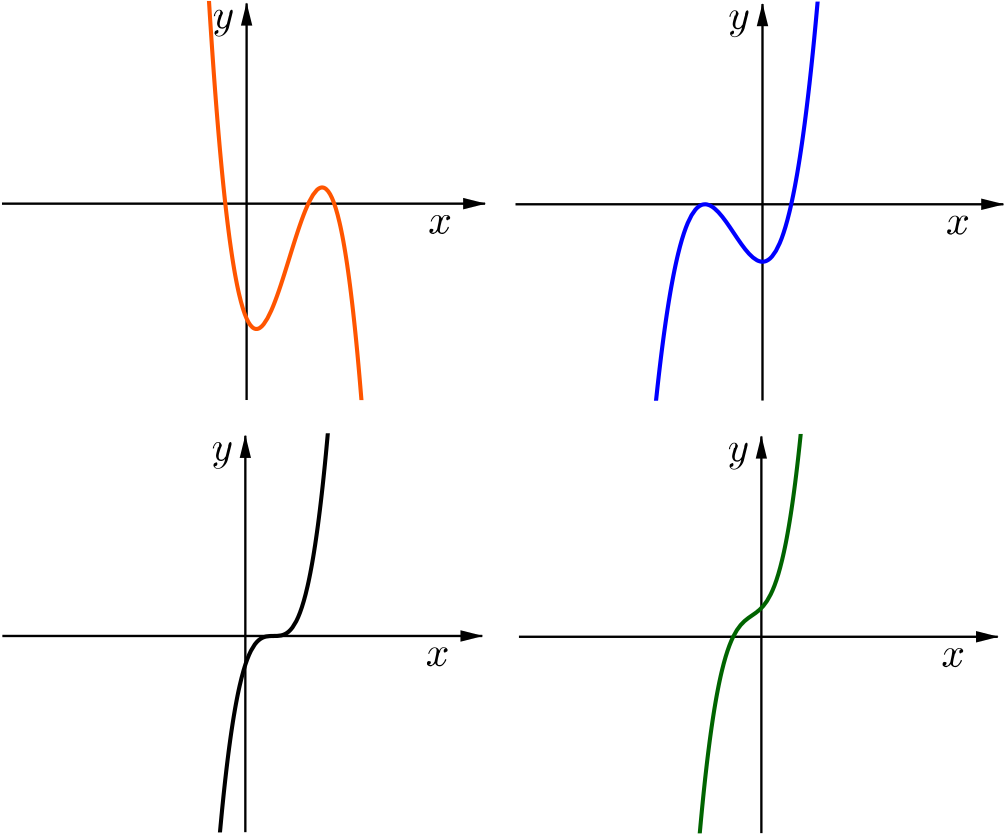
What do you know geometrically about the graph of \(f(x)\)? Sketch some different shapes that can cubic graphs be.
How many pieces of information do we need to define a cubic curve? In what form might this information be given?
Exploring coefficients and graphs
One of the standard ways to write a cubic in one variable is \(ax^3+bx^2+cx+d.\) Use the sliders for \(a,b,c\) and \(d\) to explore what happens when you vary the coefficients.
What different shapes the can the graph of \(y=ax^3+bx^2+cx+d\) be?
How many roots can a cubic have?
You might like to have a look at Curvy Cubics to explore different cubic curves further.
Any cubic can be written in the form \(ax^3+bx^2+cx+d,\) so we have four values that we can vary to give us different cubics. You may have noticed from the graphical work above, every cubic must have at least one root. If \(\alpha\) is a root, this means that \(x-\alpha\) is a factor of the cubic, so we can write our cubic as the product of \(x-\alpha\) and a quadratic, i.e. \(a(x-\alpha)(x^2+bx+c).\)
Why does having a root \(\alpha\) mean that \((x-\alpha)\) is a factor of the cubic?
What determines whether the cubic has any other roots?
Here is another GeoGebra file. You can use it to explore cubics written in a form with \(x-\alpha\) as a factor. Can you recreate the shape of the curves in the diagram above?