We will describe geometric and algebraic approaches to this problem, but you should try to combine these, rather than selecting only one of the approaches.
Can you find a cubic curve that…
- … passes through the \(x\)-axis at \(x=1\) and \(x=-1\)?
The question tells us that the graph passes through the \(x\)-axis in two places. Try to sketch a few curves that satisfy these conditions.
- … passes through the origin and touches the \(x\)-axis at \(x=-3\)?
Try to sketch some cubic curves that touch the \(x\)-axis at \(x=-3.\) How much flexibility is there if the curve also has to pass through the origin?
Parts (a) and (b) both gave information about two roots, but how did the form of this information affect the range of curves that met the criteria?
- … touches the \(x\)-axis at \(x=2\) and crosses the \(y\)-axis at \(12\)?
Now that we’ve discussed a way of tackling a couple of these questions, we can ask “How is this question different from parts (a) and (b)?” This may help you to anticipate how much choice there will be for the cubic.
We know there is a repeated root at \(x=2\), so this is a bit like part (b). But in part (b), the \(y\)-intercept was \((0,0)\) whereas in this question the \(y\)-intercept is \((0,12)\). Which \(y\)-intercept do you think gives more flexibility?
In part \((a)\) we could choose where the third root was and whether the coefficient of \(x^3\) was positive or negative. Do we have more or less freedom here?
How would your cubics for (c) be different if we had asked for a curve that crosses the \(x\)-axis at \(2\)?
- … crosses the \(y\)-axis at \(-6\) and has three integer roots?
What does the \(y\)-intercept tell us about the roots of the equation?
How much does having to have integer roots limit the possibilities?
- … crosses the \(y\)-axis at \(y=5\) and touches the \(x\)-axis at \(x=1\)?
Once again, it is worth asking how this question is similar to or different from the previous parts. Do you think there will be lots of different types of cubic curve that satisfy these conditions or only a few different types?
Given that there are infinitely many possibilities for the cubics in these questions, it is helpful to talk about different ‘types’ of cubics, so that we can try to classify the possibilities. We can choose how to define the types, depending on what the question is asking. Sometimes it may be easier to see possible groups by looking at sketches and in other cases the algebra may be more helpful.
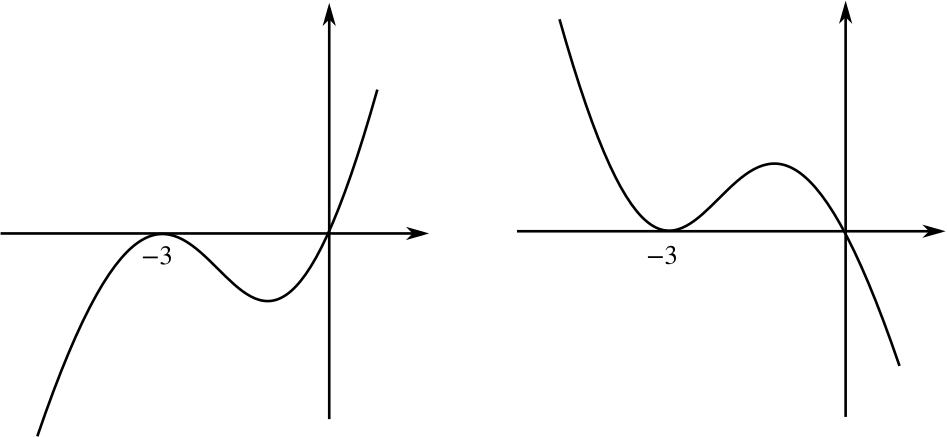
We might say that cubics are the same type if their sketch graphs look essentially the same, perhaps in terms of shape, number of roots, or whether the coefficient of \(x^3\) is positive or negative. For example, what’s the same and what’s different about these two cubics?

Looking back, the distinction between “touching” the \(x\)-axis and “crossing” it at particular points was an important idea in this problem. But if we classify cubics based on the shape of their curve, this distinction may become less important. You can explore cubics with different shaped graphs at Curvy cubics.