- Find the solution set for \(x\) given that the following three relations for \(x\), \(y\), where \(x\), \(y\in \mathbb{R}\), are simultaneously true: \[y < x+1, \quad y+6x < 20, \quad x = 5y-7.\]
A diagram of the three lines helps us visualise the problem.
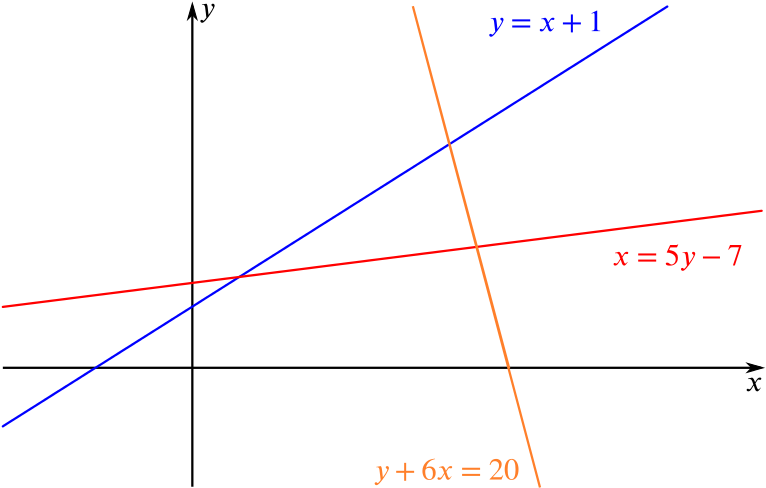
The region where y < x + 1 is the half-plane below the blue line. The blue line itself is not in the region.
The region where y + 6x < 20 is the half-plane below the yellow line. The yellow line itself is not in the region.
So we can see the portion of the red line that lies in the region where both inequalities are satisfied.
We need to find the x-values that points on this portion of red line can take.
Rearranging \(x=5y-7\) gives us \[y=\frac{x+7}{5}.\]
Substituting this into the inequalities gives \[\frac{x+7}{5}<x+1 \quad \text{and}\quad \frac{x+7}{5}+6x<20,\] from which we get \[x+7<5x+5 \quad \text{and}\quad x+7+30x<100.\] Solving these gives us \(\dfrac{1}{2}<x\) and \(x<3\) respectively. Therefore the solution set for \(x\) is \(\dfrac{1}{2} < x < 3\).
Alternatively, we could find the point of intersection of the blue line with the red line, and of the yellow line with the red line.
- Find the solution set of the inequality \[\frac{12}{x-3} < x+1, \quad (x\in \mathbb{R}, \ x \neq 3).\]
Approach 1
It’s tempting to multiply both sides by \(x-3\) to give \(12 < (x+1)(x-3)\), but \(x-3\) might be negative, and so multiplying by \(x-3\) could change the direction of the inequality.
So we split the problem up into two cases: \(x-3>0\) and \(x-3<0\).
Case 1: \(x-3>0\)
Since \(x-3>0\), we can multiply by \(x-3\) without changing the direction of the inequality to get \(12 < (x+1)(x-3)\).
This is equivalent to \(0<x^2-2x-15\), which we can rewrite as \((x-5)(x+3)>0\).
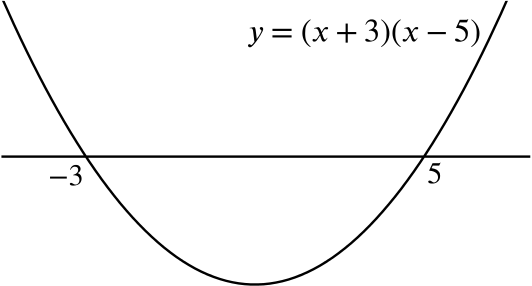
Sketching \(y=(x-5)(x+3)\) shows this inequality holds if \(x<-3\) or if \(x>5\).
Since we are only considering \(x>3\) though, the solution set is \(x>5\).
Case 2: \(x-3<0\)
Multiplying by \(x-3\) now means multiplying by a negative value, so we’ll get the same quadratic inequality, but with a different inequality sign, that is, \(0>(x-5)(x+3)\).
Referring to the sketch of \(y=(x-5)(x+3)\), this can only hold when \(-3<x<5\). As we’re only considering \(x<3\), the solution set is \(-3<x<3\).
By combining the results from the two cases, we get the solution set for \(x\) of \(-3<x<3\) or \(x>5\).
Approach 2
Since multiplying by \(x-3\) might change the sign of the inequality, we’ll multiply by something we know is never negative.
Since we want to multiply by \(x-3\) to clear the denominator, we multiply by \((x-3)^2\ge0\).
This gives us \[12(x-3)<(x+1)(x-3)^2.\]
It’s tempting to now multiply out, but instead, we can use the shared factor of \(x-3\) to rearrange and factorise.
This is a cubic which crosses the \(x\)-axis at \(3\), \(5\) and \(-3\), looking roughly like
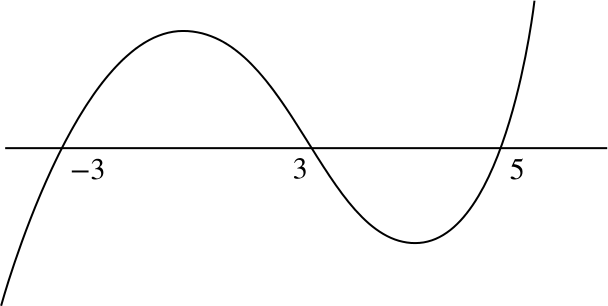
We can see that \((x-3)(x-5)(x+3)>0\) when \(-3<x<3\) or \(x>5\).
Approach 3
We begin by sketching the two functions \(y=\dfrac{12}{x-3}\) and \(y=x+1\) on the same axes.
The graph of \(y=\dfrac{12}{x-3}\) can be found from \(y=\dfrac{1}{x}\) via stretching in the \(y\)-direction by a factor of \(12\) and then translating by \(3\) in the \(x\)-direction.
So the graph looks like
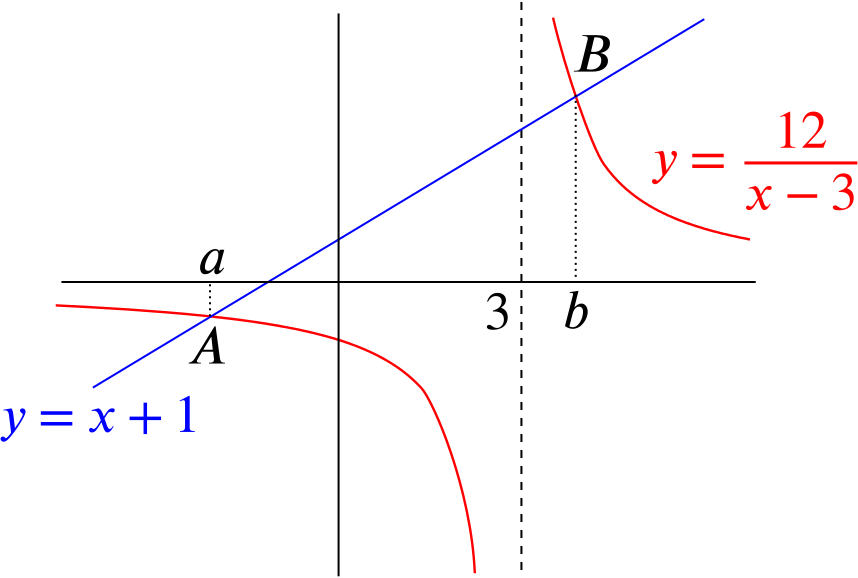
The two graphs intersect at \(A\) and \(B\), with \(x\)-coordinates \(a\) and \(b\) respectively.
It’s clear from the graph that \(\dfrac{12}{x-3} < x+1\) when the red graph is below the blue one, which occurs when \(a<x<3\) and when \(x>b\).
So it only remains to find \(a\) and \(b\), which we can do by solving the equation \[\frac{12}{x-3} = x+1.\] Multiplying by \(x-3\) and rearranging gives \[(x+1)(x-3)-12=0\] so \[x^2-2x-15=0\] which yields \((x-5)(x+3)=0\), therefore \(x=5\) or \(x=-3\).
This gives \(a=-3\) and \(b=5\), so the solution is \(-3<x<3\) or \(x>5\).
Approach 4
We have \(\dfrac{12}{x-3}<x+1\), and so bringing everything to the LHS, \(\dfrac{12}{x-3}-x-1<0\), or \(\dfrac{(x-5)(x+3)}{3-x}<0\).
As we now allow \(x\) to move from below \(-3\) to above \(5\), we can track the sign of this rational function, which gives us the same answer as before.

