Below are several statements about the quadratic equation \[ax^2 + bx + c = 0,\] where \(a\), \(b\) and \(c\) are allowed to be any real numbers except that \(a\) is not \(0\).
For each statement, decide whether MUST, MAY or CAN’T is the correct word to use in the statement.
To say that something MUST be the case, we need it to be true in all cases; we will need to give a convincing explanation (a proof) of why this must be always true.
To show that something CAN’T be the case, we likewise need to give a convincing explanation (a proof) of why.
To show that something MAY be the case, we need to give an example when it is true and an example when it is false. If you want a harder challenge, can you determine exactly when it is and when it is not true?
You may like to explore some of the scenarios on the cards using graphing software or the interactive graph in this resource.
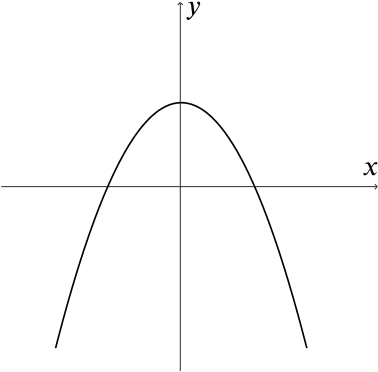
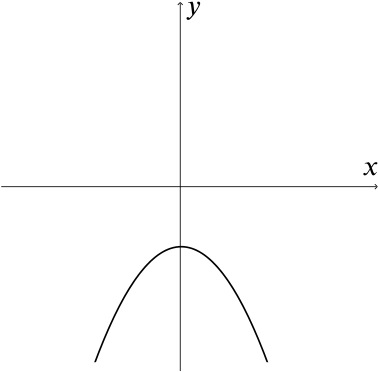
- If \(a < 0\), then \(ax^2+bx+c=0\)
MUST / MAY / CAN’T have real roots.
Knowing that \(a<0\) tells us that this is a “vertex up” parabola. For example, it could look like one of these two graphs:
|
|
The graph of the left is a sketch of \(y=-x^2+1\), while the one on the right is \(y=-x^2-1\).
This shows that if \(a < 0\), then \(ax^2+bx+c=0\) MAY have real roots.
- If \(b^2 - 4ac = 0\), then \(ax^2+bx+c=0\)
MUST / MAY / CAN’T have one repeated real root.
From the quadratic formula, we know that the equation \(ax^2 + bx + c = 0\) (with \(a \neq 0\)) has roots \[x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}.\] In this case, we are told that the discriminant \(b^2 - 4ac\) is \(0\), so the only real root of the equation is \(x = \frac{-b}{2a}\).
Therefore, if \(b^2 - 4ac = 0\), then \(ax^2+bx+c=0\) MUST have one repeated real root.
- If \(ax^2+bx+c=0\) has no real roots, then \(ax^2 + bx - c = 0\)
MUST / MAY / CAN’T have two distinct real roots.
If the equation has no real roots, then the graph of \(y=ax^2+bx+c\) (which intersects the \(y\)-axis at \(c\)) does not cut the \(x\)-axis, and its vertex is on the same side of the \(x\)-axis as \(c\), as in the following sketches, the left one showing the case of \(a>0\) and the right one showing \(a<0\):
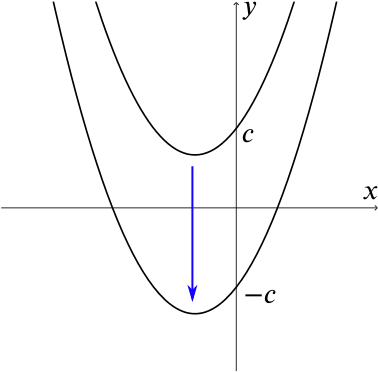
|
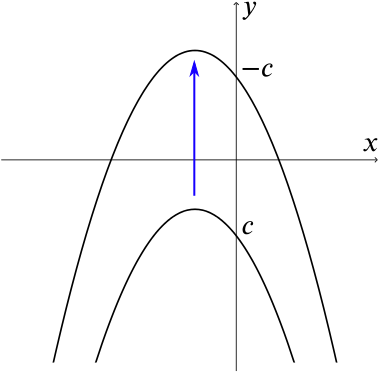
|
The graph of \(y=ax^2+bx-c\) is obtained by translating the first graph in the \(y\)-direction until it intersects the \(y\)-axis at \(-c\). Since the direction of the parabola does not change (it remains “vertex up” or “vertex down”), it must now intersect the \(x\)-axis in two distinct points.
Therefore, if \(ax^2+bx+c=0\) has no real roots, then \(ax^2 + bx - c = 0\) MUST have two distinct real roots.
Alternatively, we can argue algebraically. Since the equation \(ax^2 + bx + c = 0\) has no real roots, we can say something about the discriminant: we know that \(b^2 - 4ac < 0\).
Since \(b^2\) is the square of a real number, it is always non-negative (that is, \(b^2 \geq 0\)), so \(b^2 < 4ac\) tells us that \(4ac\) is positive.
The equation \(ax^2 + bx - c = 0\) has discriminant \(b^2 + 4ac\), and now this must be positive.
So \(ax^2 + bx - c = 0\) has two distinct real roots.
- If \(\frac{b^2}{a} < 4c\), then \(ax^2+bx+c=0\)
MUST / MAY / CAN’T have two distinct real roots.
The tempting thing to do is to multiply both sides of the inequality by \(a\), to obtain \(b^2<4ac\). This would give \(b^2-4ac<0\), so that the equation couldn’t have two distinct real roots – it would have no real roots.
Unfortunately, we don’t know whether \(a\) is positive or negative, so when we multiply both sides of the inequality by \(a\), we may be changing the direction of the inequality.
If \(a\) is positive, then \(b^2<4ac\) and the equation has no real roots.
However, if \(a\) is negative, then multiplying the given inequality by \(a\) will yield \(b^2>4ac\), so \(b^2-4ac>0\) and the equation has two distinct real roots.
So if \(\frac{b^2}{a} < 4c\), then \(ax^2+bx+c=0\) MAY have two distinct real roots, depending upon the sign of \(a\).
- If \(b = 0\), then \(ax^2+bx+c=0\)
MUST / MAY / CAN’T have one repeated real root.
If we start by taking \(a=1\), then we have the family of quadratics \(y=x^2+c\), which look like this:
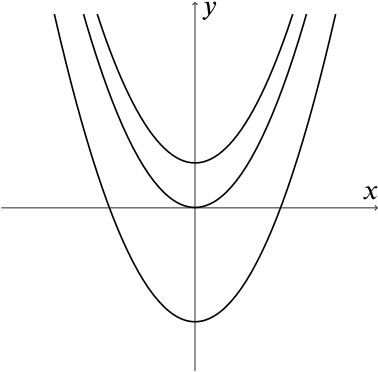
We can clearly see that we may have two real roots, one repeated real root (when \(c=0\)) or no real roots.
So if \(b = 0\), then \(ax^2+bx+c=0\) MAY have one repeated real root.
Alternatively, we could consider this from an algebraic perspective.
The discriminant is \(b^2-4ac=-4ac\), since \(b=0\). For the equation to have one repeated real root, we require the discriminant to be zero. This will be true if and only if \(c=0\) (as \(a\ne0\)), so \(ax^2+bx+c=0\) MAY have one repeated real root.
- The equation \(ax^2+bx+c=0\)
MUST / MAY / CAN’T have three real roots.
The equation CAN’T have three real roots, as a quadratic equation can have at most two roots. (We can see this from the quadratic formula or from thinking about the shape of the graph.)
- If \(c = 0\), then \(ax^2+bx+c=0\)
MUST / MAY / CAN’T have real roots.
If \(c = 0\), then the equation is of the form \(ax^2 + bx = x(ax + b) = 0\), and so \(x = 0\) is a real root.
In fact \(x = - \frac{b}{a}\) is also a real root, so if \(b \neq 0\) then the equation has two distinct real roots, while if \(b=0\), it has one repeated real root.
Alternatively, we could calculate the discriminant, \(b^2-4ac=b^2\) (since \(c=0\)). Since \(b^2\) is a square, it is never negative, so the equation always has either two distinct or one repeated real root.
So if \(c = 0\), then \(ax^2+bx+c=0\) MUST have real roots.
- The equation \(ax^2+bx+c=0\)
MUST / MAY / CAN’T have the same number of real roots as \(ax^2 - bx + c = 0\).
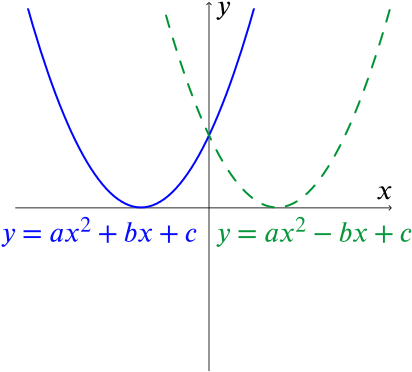
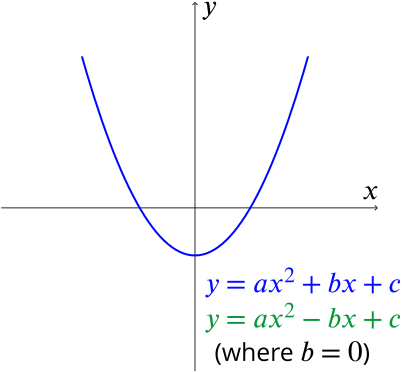
Changing the \(+bx\) term to \(-bx\) in the equation \(y=ax^2+bx+c\) has the same effect as replacing \(x\) by \(-x\) (since \(a(-x)^2=ax^2\)).
So the effect on the graph of \(y=ax^2+bx+c\) is to reflect it in the \(y\)-axis, as in the following sketches:
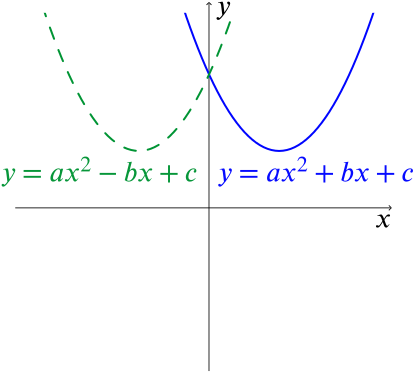
|
|
|
So we see that \(ax^2+bx+c=0\) and \(ax^2-bx+c=0\) MUST have the same number of real roots. We can even see more than this: the roots of \(ax^2-bx+c=0\) are the negatives of the roots of \(ax^2+bx+c=0\).
Alternatively, we could think in terms of the discriminant.
The equations \(ax^2 + bx + c = 0\) and \(ax^2 - bx + c = 0\) both have discriminant \(b^2 - 4ac\), so they must have the same number of real roots (whatever that number is).
- If \(ax^2+bx+c=0\) has two distinct real roots, then we
MUST / MAY / CAN’T have \(ac < \frac{b^2}{4}\).
If the equation has two distinct real roots, then its discriminant must be positive, that is, \(b^2 - 4ac > 0\).
Now we can rearrange that to obtain \(4ac < b^2\). We can now divide this inequality by \(4\) (which is positive) to obtain \(ac < \frac{b^2}{4}\).
So if \(ax^2+bx+c=0\) has two distinct real roots, then we MUST have \(ac < \frac{b^2}{4}\).
- If \(c > 0\), then \(ax^2+bx+c=0\)
MUST / MAY / CAN’T have two distinct real roots.
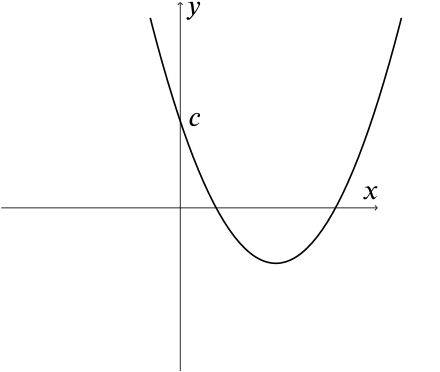
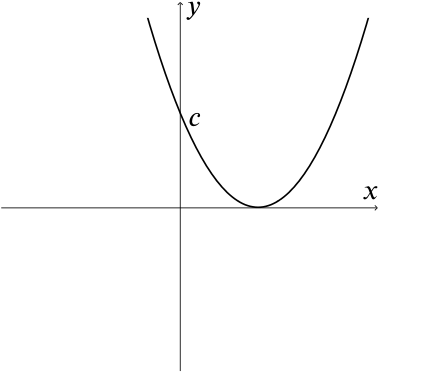
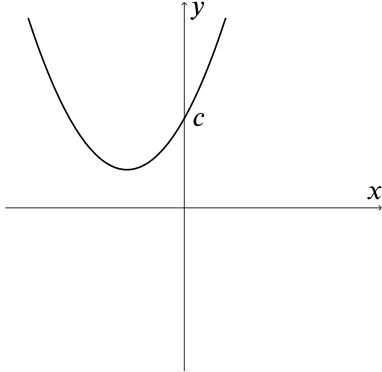
The value of \(c\) tells us where the quadratic crosses the \(y\)-axis. Here are some sketches of graphs with a positive \(y\)-intercept.
|
|
|
So we can see from this that if \(c > 0\), then \(ax^2+bx+c=0\) MAY have two distinct real roots.
Explicit examples of quadratic equations would include \(x^2 - 3x + 2 = (x-1)(x-2) = 0\), which has two distinct real roots, and \(x^2+1=0\), which has no real roots.
Alternatively, if we consider the discriminant \(b^2-4ac\), if we take \(a>0\), then \(4ac\) is positive. So if we choose \(b\) with \(b^2>4ac\), we will have \(b^2-4ac>0\) (giving two distinct real roots), while if we choose \(b\) with \(0\le b^2<4ac\), then \(b^2-4ac<0\) and there are no real roots.
- The equation \(ax^2+bx+c=0\)
MUST / MAY / CAN’T have the same number of real roots as \(cx^2 + bx + a = 0\).
There is no obvious way of relating the graph of \(y=ax^2+bx+c\) to that of \(y=cx^2+bx+a\), though it would be fine to draw them both and compare them.
We consider instead the discriminants of the two equations. The discriminant of \(ax^2+bx+c=0\) is \(b^2-4ac\), while that of \(cx^2+bx+a=0\) is \(b^2-4ca\). So the discriminants are equal, and so the equations have the same number of roots.
However, we made an assumption here which may not be valid. The equation \(ax^2+bx+c=0\) is certainly a quadratic, as \(a\) is non-zero. However, \(cx^2+bx+c=0\) is only a quadratic if \(c\) is non-zero. But what if \(c=0\)? In this case, \(cx^2+bx+a=0\) is just the linear equation \(bx+a=0\) (assuming \(b\) is non-zero). So if \(c=0\), the equation \(cx^2+bx+a=0\) has one real root, which will not be the same number of real roots as \(ax^2+bx+c=0\).
As explicit examples, the equation \(x^2 - 3x + 2 = (x-1)(x-2) = 0\) has two distinct real roots. The equation obtained by reversing the coefficients is \(2x^2 - 3x + 1 = 0\), and this factorises as \(2x^2 - 3x + 1 = (2x - 1)(x - 1) = 0\) so has roots \(1\) and \(\frac{1}{2}\)—it too has two distinct real roots.
On the other hand, the equation \(x^2 - x = 0\) has two distinct real roots (since \(x^2 - x = x(x-1) = 0\), which has roots \(x = 0\) and \(x = 1\)). The equation obtained by reversing the coefficients is \(0x^2 - x + 1 = 0\), that is, \(-x + 1 = 0\), and this has just one real root (\(x = 1\)).
Therefore, the equation \(ax^2+bx+c=0\) MAY have the same number of real roots as \(cx^2 + bx + a = 0\).
- If \(ax^2+bx+c=0\) has no real roots, then \(-ax^2 - bx - c = 0\)
MUST / MAY / CAN’T have two distinct real roots.
One way to think about this is that the graph of \(y=-ax^2-bx-c\) is the reflection of the graph \(y=ax^2+bx+c\) in the \(x\)-axis. They therefore have the same number of roots as each other.
These two graphs show examples of this. On the left, \(y=(x-1)(x-2)\) has two real roots; on the right, \(y=x^2+1\) has none. It is clear that their reflections have the same number of real roots.

|
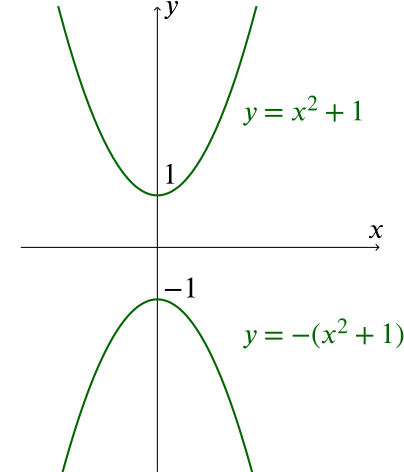
|
Algebraically, if we multiply \(-ax^2-bx-c=0\) by \(-1\), we obtain \(ax^2+bx+c=0\), which must therefore have the same roots as the original equation. In some sense, they are essentially the same equation.
Therefore, if \(ax^2+bx+c=0\) has no real roots, then \(-ax^2 - bx - c = 0\) CAN’T have two distinct real roots.

