The diagonals of the square \(ABCD\) meet at \(O\).
The bisector of angle \(OAB\) meets \(BO\) and \(BC\) at \(N\) and \(P\) respectively.
The length of \(NO\) is \(24\).
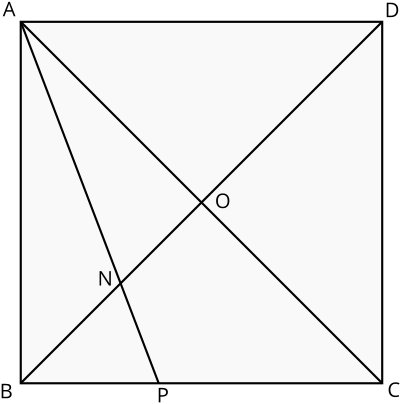
How long is \(PC\)?
How many ways can you find to answer this question? As you progress along the Geometry line, you will learn new techniques that will give other approaches to this problem, so this is a good one to bookmark and revisit from time to time to see what else you can do.

