The diagonals of the square \(ABCD\) meet at \(O\).
The bisector of angle \(OAB\) meets \(BO\) and \(BC\) at \(N\) and \(P\) respectively.
The length of \(NO\) is \(24\).
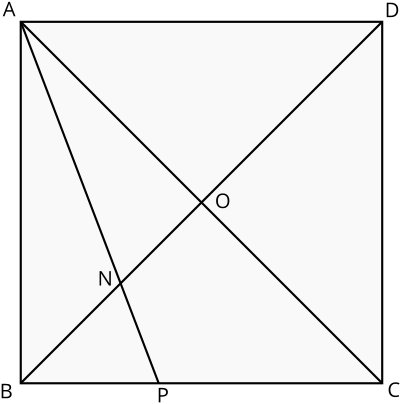
How long is \(PC\)?
Since this is a station with a focus on similar triangles, perhaps we can look for a solution to the problem using similar triangles (although there are lots of other approaches too).
There are lots of triangles in the diagram. Can you find any similar triangles that might help?
Which angles are the same in the diagram? Does that lead you to find any more interesting triangles?

