The diagonals of the square \(ABCD\) meet at \(O\).
The bisector of angle \(OAB\) meets \(BO\) and \(BC\) at \(N\) and \(P\) respectively.
The length of \(NO\) is \(24\).
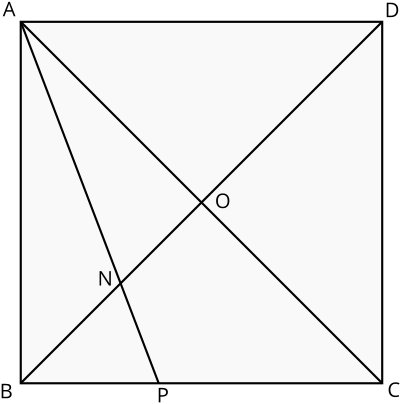
How long is \(PC\)?
There are many ways to solve this problem. We’ll give one solution in detail here, and suggest some other approaches that you could investigate as you meet new ideas later on the Geometry line.
Method 1
The question doesn’t tell us the side length of the square, but it seems like that might be an important quantity so let’s give it a name and see whether it’s relevant later on.
Let the square have side length \(x\). Then the diagonals have length \(x \sqrt{2}\), and \[BO = \frac{x \sqrt{2}}{2} = \frac{x}{\sqrt{2}}.\]
We see that triangles \(AON\) and \(ABP\) are similar (they both have a right angle and one of the other angles is \(\frac{1}{2}\angle BAO\) so they have the same angles).
Here’s a tip when dealing with similar triangles. When we said that triangles \(AON\) and \(ABP\) are similar, the points were in the right order. That is, vertex \(A\) in triangle \(AON\) corresponds to vertex \(A\) in triangle \(ABP\), vertex \(O\) in triangle \(AON\) corresponds to vertex \(B\) in triangle \(ABP\), and vertex \(N\) in triangle \(AON\) corresponds to vertex \(P\) in triangle \(ABP\). Being careful about that ordering when we wrote down the similar triangles makes it easier to be clear about which sides of the triangles correspond.
Now \[\frac{BP}{AB} = \frac{ON}{AO},\] so \[BP = AB \times \frac{ON}{AO} = \frac{24x}{x/\sqrt{2}} = 24\sqrt{2}.\]
The triangle \(BNP\) is interesting because it involves the lengths \(BN\) and \(BP\), which are important in this question. Let’s think about the angles in that triangle.
We have \(\angle BAP = \angle PAC = 22.5^{\circ}\) (because \(AP\) is the angle bisector of angle \(BAC\), and that is \(45^{\circ}\)). Now triangle \(BAP\) is right-angled, and the sum of the angles in the triangle is \(180^{\circ}\), so \[\angle BPA = 180^{\circ} - 90^{\circ} - 22.5^{\circ} = 67.5^{\circ}.\] We can also find \(\angle BNP\), as we know that \(\angle NBP = 45^{\circ}\). Looking at the angles in triangle \(BNP\), we have \[\angle BNP = 180^{\circ} - \angle NBP - \angle BPN = 67.5^{\circ}.\]
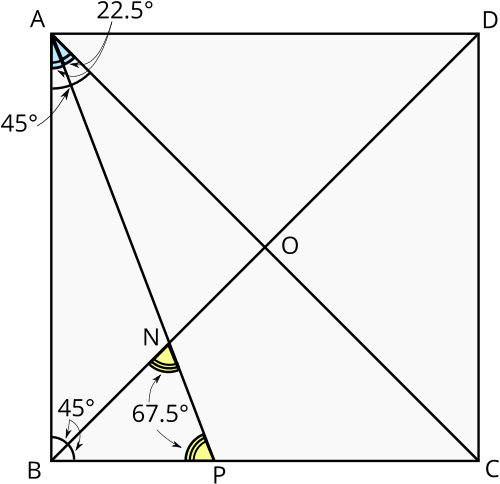
We have shown that \(\angle BPA = \angle BNP\), so triangle \(BNP\) is isosceles, so \(BN = BP = 24\sqrt{2}\) (using our earlier calculation).
We could use this to find the length \(x\) (using \(BN + NO = BO\) and our expressions for those three lengths), but in fact we do not need to find \(x\) in order to complete the question.
We see that triangles \(APC\) and \(ANB\) are similar (they each contain an angle of \(45^{\circ}\) and an angle of \(22.5^{\circ}\), so have all angles the same), so \[\frac{PC}{AC} = \frac{NB}{AB},\] so \[PC = AC \times \frac{NB}{AB} = \frac{x \sqrt{2} \times 24 \sqrt{2}}{x} = 48.\]
Here is another argument using similar triangles. The argument is perhaps simpler and more elegant, but involves thinking of constructing another point and line.
Method 2
Let \(R\) be the point of intersection of the line \(AP\) with the line through \(C\) parallel to \(ON\).
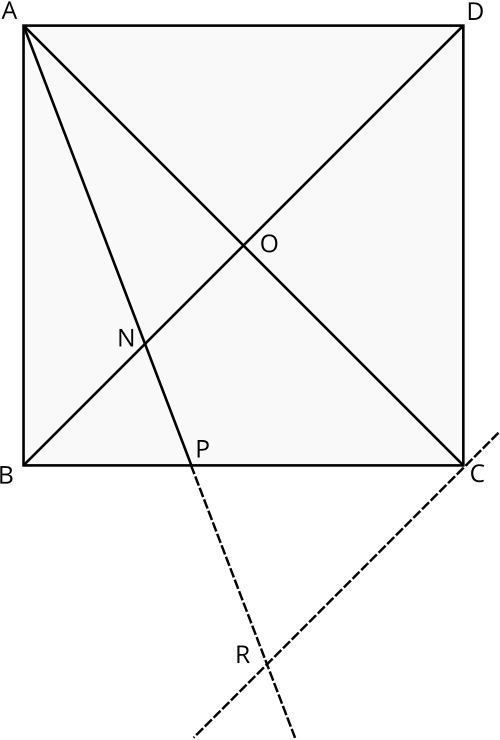
Then \(\angle ACR = 90^{\circ}\), so triangles \(AON\) and \(ACR\) are both right-angled, and they share the angle at \(A\), so their angles are the same and so they are similar. This shows that \[\frac{CR}{ON} = \frac{AC}{AO} = 2,\] so \(CR = 2 \times ON = 2 \times 24 = 48\).
It’s not clear that this will be helpful, unless we can find a way to relate \(CR\) to \(PC\)…
We haven’t yet used the fact that the line \(AP\) bisects the angle \(BAO\), so we should try to use that.
Since the line \(AP\) is the bisector of angle \(BAO\), we see that \(\angle NAO = 22.5^{\circ}\), and so \[\angle ANO = \angle ARC = 180^{\circ} - 90^{\circ} - 22.5^{\circ} = 67.5^{\circ}.\] Also, \[\angle RPC = 180^{\circ} - \angle PRC - \angle PCR = 180^{\circ} - 67.5^{\circ} - (90^{\circ} - 45^{\circ}) = 67.5^{\circ}.\]
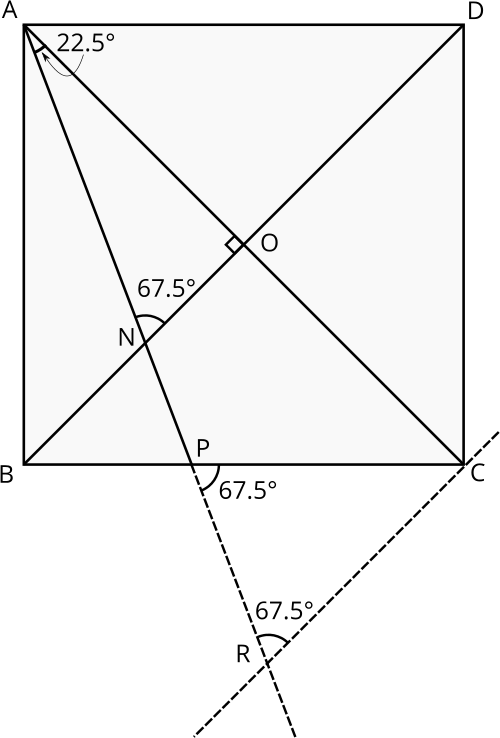
This means that triangle \(CRP\) is isosceles, and so \[PC = RC = 48.\]
Here are some starting points for other possible approaches.
Method 3
Write \([XYZ]\) for the area of triangle \(XYZ\).

Triangles \(BAP\) and \(PAC\) have the same height, so their areas are in the same ratio as their bases: \[\frac{[BAP]}{[PAC]} = \frac{BP}{PC}.\] But we can also compute the areas in another way, using the ‘\(\frac{1}{2}ab\sin C\)’ formula. For convenience, let \(\theta = \angle BAP\) (so \(\theta = 22.5^{\circ}\), although that does not matter here). We get \[\frac{[BAP]}{[BAC]} = \frac{\frac{1}{2}AB \times AP \sin\theta}{\frac{1}{2}AP \times AC \sin\theta}.\]
Can you complete the argument?
Method 4

Triangle \(ABP\) is right-angled, so we can use trigonometry. Since \(\angle BAP = 22.5^{\circ}\), we see that \[BP = AB \tan(22.5^{\circ}).\] We can use a double angle formula for \(\tan(2 \theta)\) to find \(\tan(22.5^{\circ})\), since we know the value of \(\tan(45^{\circ})\).
Can you complete the argument?

