Three points have co-ordinates \(P\,(-2, -3)\), \(Q\,(2, 0)\), \(R\,(8, -8)\).
- Prove that \(\widehat{PQR}=90^\circ\).
Two lines are perpendicular if their gradients multiply to \(-1\). Consider the figure
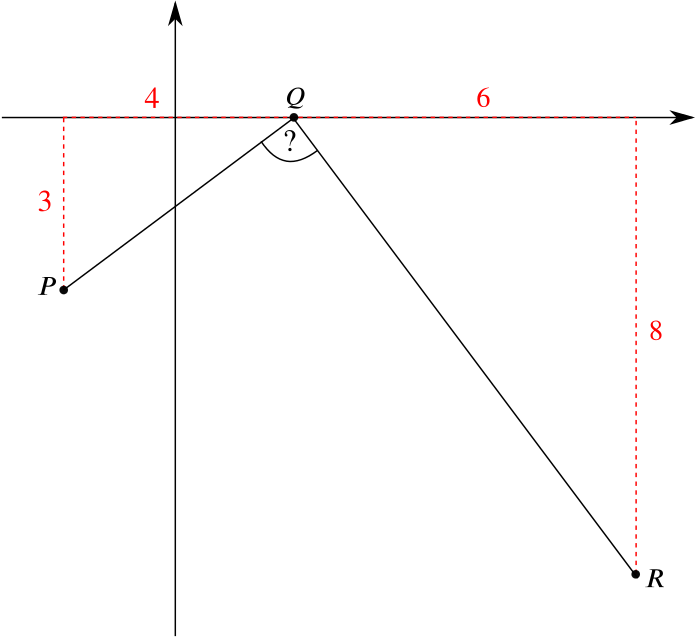
The horizontal and vertical distances are shown in red. The gradient of the line \(PQ\) is \(\dfrac{3}{4}\), and the gradient of the line \(QR\) is \(-\dfrac{8}{6}=-\dfrac{4}{3}\). As these gradients multiply to \(-1\), the angle \(\widehat{PQR}\) is \(90^\circ\).
- Calculate the area of \(\Delta PQR\).
The area of a triangle is \(\dfrac{base \times height}{2}\). In our case the base and height are the sides \(a\) and \(b\) as shown in the following diagram.
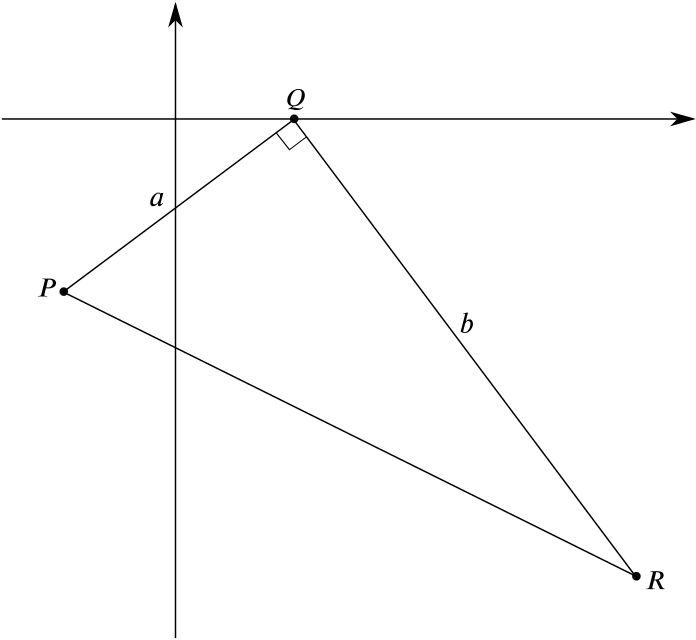
By considering the red triangles drawn in part (i) we can use Pythagoras’ Theorem to compute the length of \(a\) and \(b\). Using this we get \[a^2 = 3^2 + 4^2 \quad \text{ and } \quad b^2 = 6^2 + 8^2.\] This yields \[a = \sqrt{3^2 + 4^2} = \sqrt{25}=5,\] and \[b = \sqrt{6^2 + 8^2} = \sqrt{100} = 10.\] Therefore, the area of \(\Delta PQR\) is \(\dfrac{5 \times 10}{2} = 25\).
- Calculate the length of \(PR\) and hence, or otherwise, find the perpendicular distance of \(Q\) from \(PR\).
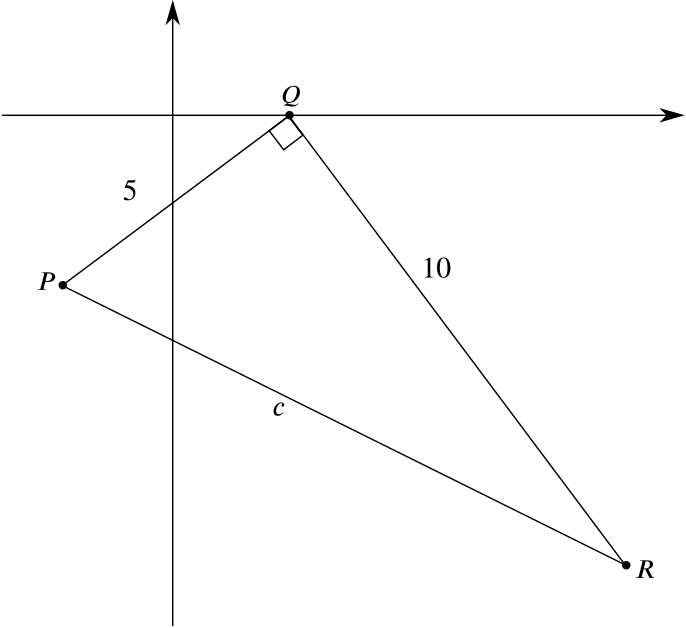
We can use Pythagoras’ Theorem once more to compute the length of \(PR\).
We know that \(a = 5\) and \(b = 10\), so by Pythagoras’ Theorem, \(c^2 = 5^2 + 10^2\) and \(c = \sqrt{5^2 + 10^2} = \sqrt{125}= 5\sqrt{5} (\approx 11.18)\).
The perpendicular distance of \(Q\) from \(PR\) is shown in the following diagram, where we call it \(h\).
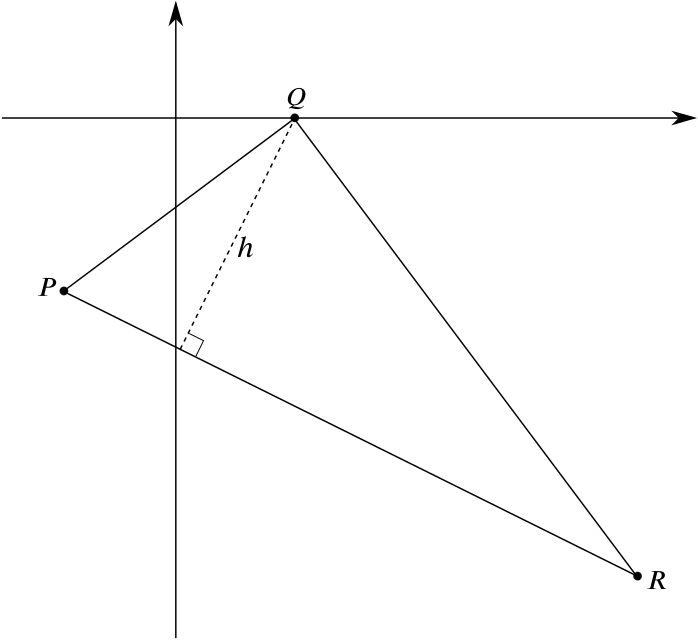
Notice that \(h\) is the height of the triangle \(\Delta PQR\) with base \(PR\) as \(h\) is perpendicular to \(PR\).
By the formula for the area of a triangle given in part (ii), and knowing that the area of the triangle is \(25\), we have \(\dfrac{c \times h}{2} = 25\).
Hence \(\dfrac{5\sqrt{5} \times h}{2} = 25\) and therefore \[h = \frac{50}{5\sqrt{5}} = \frac{10}{\sqrt{5}} = \sqrt{\frac{100}{5}} = \sqrt{20} = 2\sqrt{5} (\approx 4.47),\] and so the exact perpendicular distance of \(Q\) from \(PR\) is \(2\sqrt{5}\).

