You may recall the spider from Part 1. It is sitting in the middle of one of the smallest walls in my living room, and a fly is resting by the side of the window on the opposite wall, some way above the floor and \(\quantity{0.5}{m}\) from the adjacent wall.
The room is \(\quantity{8}{m}\) long, \(\quantity{4}{m}\) wide and \(\quantity{3}{m}\) high.
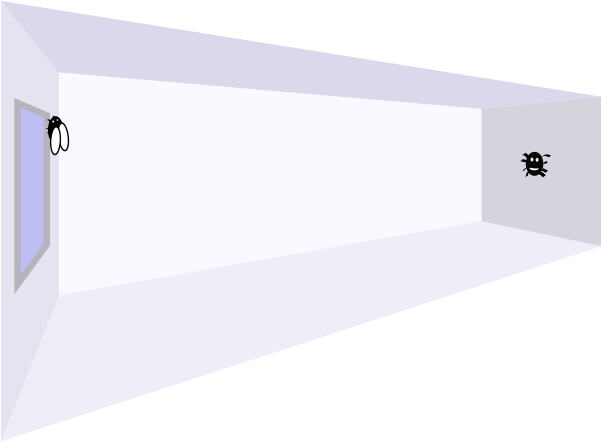
This time, the fly is at a height \(h\,\text{m}\) above the floor.
What is the shortest distance the spider could crawl to reach the fly?
How does the spider’s best route depend on \(h\)?
What different possible routes are there?
Are there some possible routes that I can reject immediately?
How can I use symmetry to simplify the problem a little?

