You may recall the spider from Part 1. It is sitting in the middle of one of the smallest walls in my living room, and a fly is resting by the side of the window on the opposite wall, some way above the floor and \(\quantity{0.5}{m}\) from the adjacent wall.
The room is \(\quantity{8}{m}\) long, \(\quantity{4}{m}\) wide and \(\quantity{3}{m}\) high.
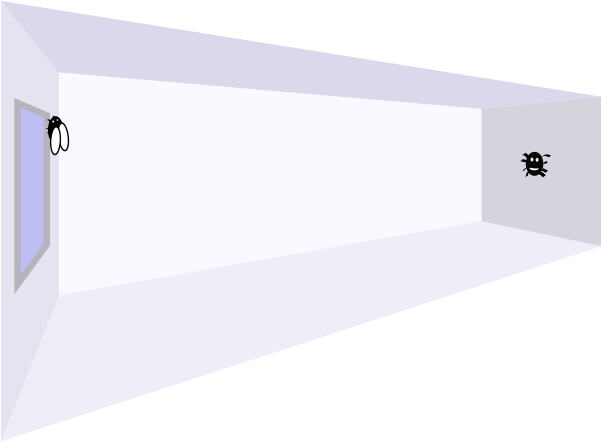
This time, the fly is at a height \(h\,\text{m}\) above the floor.
What is the shortest distance the spider could crawl to reach the fly?
How does the spider’s best route depend on \(h\)?
As we saw in the solution to Part 1, there are a number of possible routes: the nearby side wall route, the ceiling route and two possible combinations of these. In part 1, we did not even consider the floor route, as the fly is nearer to the ceiling than the floor. But now, as the fly may be nearer the floor, we need to consider routes involving the floor as well.
Using symmetry
A crucial insight in the above paragraph was that we can ignore the floor route if the fly is above the middle of the room, because the spider is in the very centre of the end wall. This suggests to us that the problem has symmetry.
If we reflect the whole room from top to bottom, we see that the fly being \(\quantity{h}{m}\) above the floor is essentially the same as it being \(\quantity{h}{m}\) below the ceiling, just with the roles of the floor and ceiling switched:
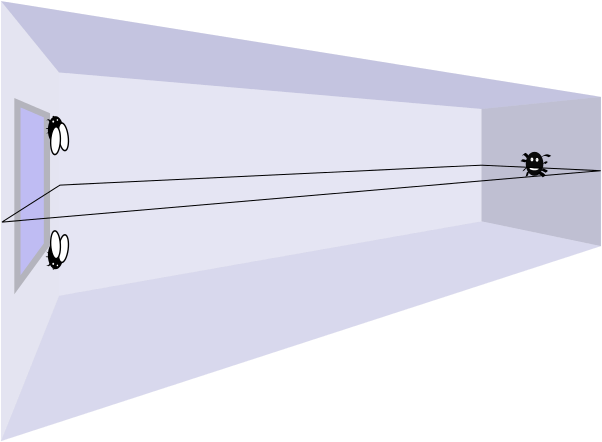
So if we solve the problem for the fly being in the top half of the room \(\quantity{h}{m}\) above the floor, then we automatically know the solution when the fly is in the bottom half \(\quantity{(3-h)}{m}\) above the floor.
The room is \(\quantity{3}{m}\) high, so the top half corresponds to \(h\ge 1.5\) and the bottom half to \(h\le 1.5\).
Since we looked at the case \(h=2\) in Part 1, which was closer to the ceiling, we will continue that work and consider the case where the fly is in the top half of the room, so \(h\ge 1.5\).
The possible routes and their lengths
As we saw in the solution to Part 1, there are four possible routes. We work out the length of each of them again, this time with the fly being at a height \(\quantity{h}{m}\) above the floor.
In Part 1, we rejected the route via the side wall and then the ceiling as it was obviously longer than the side wall route. It is not clear whether that is the case for all values of \(h\), so we include it for consideration here.
However, we can still reject any routes which involve the spider travelling via the other side wall (the one nearer to us in the picture), since the spider is nearer to the far side wall. With a little bit of thought, it is also possible to see that the spider should not follow a route which passes through both the floor and the ceiling via the side wall, as that will be longer than the route via only the ceiling.
In the following nets, we have indicated the length \(h\) with a thick green line, and marked it \(h\). We call the distances that the spider walks along the different routes \(d_1\), \(d_2\), \(d_3\) and \(d_4\) for ease of later reference.
Route 1: via the side wall
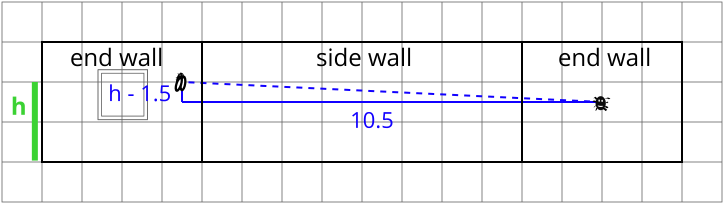
\[d_1=\text{distance the spider walks}=\sqrt{10.5^2+(h-1.5)^2}= \sqrt{h^2-3h+112.5}.\]
(Note that the spider is above the midpoint, so \(h\ge 1.5\). If the spider were below the midpoint, we would have to replace the length \(h-1.5\) by \(1.5-h\).)
Route 2: via the ceiling
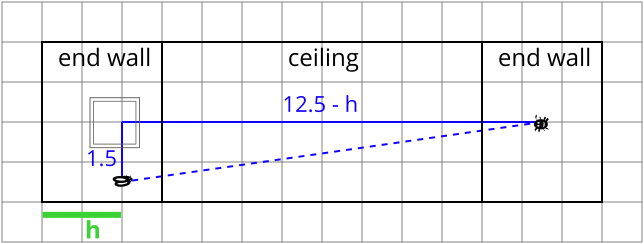
\[d_2=\text{distance the spider walks}=\sqrt{1.5^2+(12.5-h)^2}= \sqrt{h^2-25h+158.5}.\]
Route 3: via the ceiling and then the wall
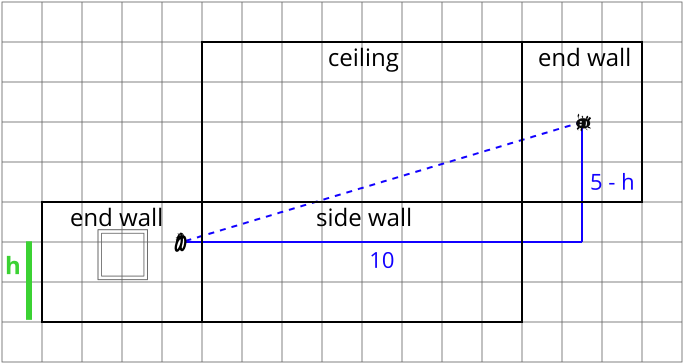
\[d_3=\text{distance the spider walks}=\sqrt{10^2+(5-h)^2}= \sqrt{h^2-10h+125}.\]
Route 4: via the wall and then the ceiling
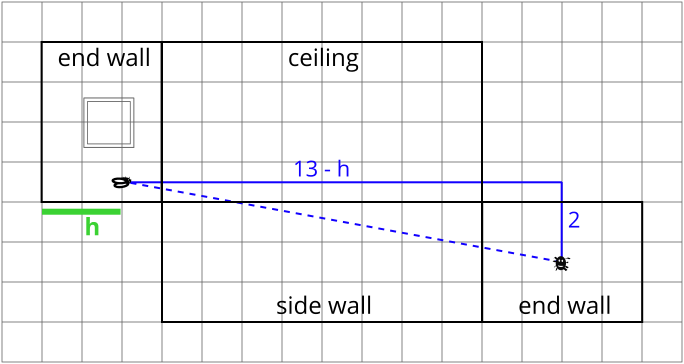
\[d_4=\text{distance the spider walks}=\sqrt{2^2+(13-h)^2}= \sqrt{h^2-26h+173}.\]
Comparing the routes
Now that we have all four possible routes, we need to determine which is the shortest. We only need to compare the squares of the distances, so we can ignore the square root signs. (This is because if \(a\) and \(b\) are positive, then \(\sqrt{a}<\sqrt{b}\) if and only if \(a<b\).) We have \[\begin{align*} d_1^2 &= h^2-\phantom{0}3h+112.5\\ d_2^2 &= h^2-25h+158.5\\ d_3^2 &= h^2-10h+125\\ d_4^2 &= h^2-26h+173 \end{align*}\] We see that they all have an identical \(h^2\) term, so we might as well subtract this and just compare the linear parts; we write \(y_1=d_1^2-h^2\) and so on: \[\begin{align*} y_1 &= 112.5- 3h\\ y_2 &= 158.5-25h\\ y_3 &= 125 -10h\\ y_4 &= 173 -26h \end{align*}\]We are interested in the range \(1.5\le h\le 3\) (the fly is in the upper half of the room).
Comparing these still looks a little tricky, so we use graph-plotting software to draw the four graphs; this will give us a good idea of what is going on and save us from having to do lots of unnecessary algebra.
This is the resulting graph. (The \(h\)-axis extends beyond \(1.5\) and \(3\) for convenience, even though \(h\) can only take values between them.)
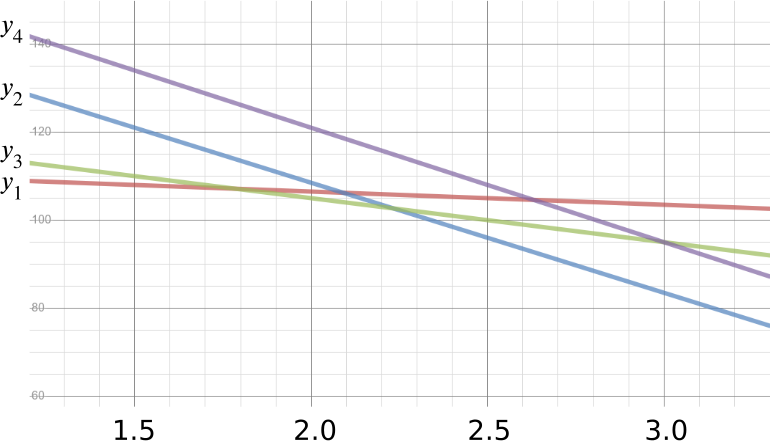
From the graph, we see that Route 1 is shortest for \(1.5\le h<1.8\) (or thereabouts), then Route 3 is the shortest until \(h\approx 2.25\). Then Route 2 is shortest until \(h=3\). Route 4, via the wall and then the ceiling, is never shortest.
To find the transition points exactly, we need only solve equations such as \(y_1=y_3\) to find where Route 1 and Route 3 are equal in length, and similarly for when Routes 3 and 2 are the same length.
If we had not used graph-plotting software, we would have been forced to work purely algebraically. We would have had to compare several other pairs of lines, so the software has saved us lots of needless effort.
The first transition occurs when \(y_1=y_3\): we can substitute our formulae for \(y_1\) and \(y_3\) in to get \[112.5- 3h=125 -10h\] which gives \(7h=12.5\), so \(h=1.79\) to 2 d.p.
The second transition occurs when \(y_3=y_2\), giving \[125 -10h=158.5-25h,\] so \(15h=33.5\), so \(h=2.23\) to 2 d.p.
Using symmetry and finishing off
We now know that Route 2, the ceiling route, is best for heights in the range \(\quantity{2.23}{m}\) to \(\quantity{3}{m}\). Thus by symmetry, the floor route is best for heights in the range the range \(\quantity{0}{m}\) to \(\quantity{0.77}{m}\).
Route 3, via the ceiling and then the side wall, is best for heights in the range \(\quantity{1.79}{m}\) to \(\quantity{2.23}{m}\). By symmetry, therefore, the route via the floor and then the side wall will be best for heights in the range \(\quantity{0.77}{m}\) to \(\quantity{1.21}{m}\).
Finally, Route 1, via the side wall, is best for heights in the range \(\quantity{1.5}{m}\) to \(\quantity{1.79}{m}\), and by symmetry, also for heights in the range \(\quantity{1.21}{m}\) to \(\quantity{1.5}{m}\). We can combine these ranges, and deduce that the side wall route is best for heights in the range \(\quantity{1.21}{m}\) to \(\quantity{1.79}{m}\).

