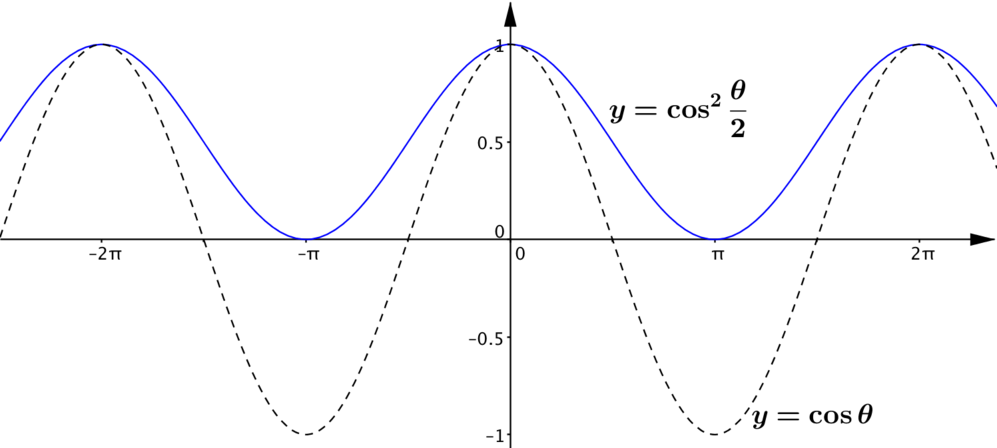
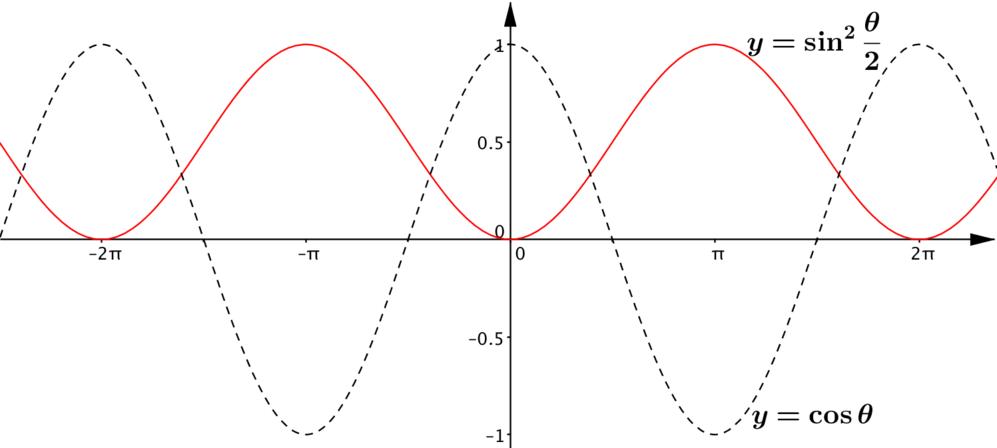
Take a look at these identities.
\[ \cos^2 \frac{\theta}{2} \equiv \frac{1}{2}(1+\cos \theta) \quad \quad \quad \sin^2 \frac{\theta}{2} \equiv \frac{1}{2}(1-\cos \theta)\]
How could you use these identities to help you sketch graphs of \(y=\cos^2 \frac{\theta}{2}\) and \(y=\sin^2 \frac{\theta}{2}\)?
These ideas may help you to sketch the graphs of \(y=\cos^2 \frac{\theta}{2}\) and \(y=\sin^2 \frac{\theta}{2}\)
As the left-hand side is a square in each case, we know the right hand sides must be zero or positive. This is fine, because \(-1\leq \cos \theta \leq 1\), so \(1+\cos \theta\) will be at least \(0\) and at most \(2\). Similarly, \(1-\cos \theta\) must be between \(0\) and \(2\).
The right-hand sides of the identities are the same except for a minus sign, so we’d expect the behaviour of the two functions to be very similar, but the maximum and minimum values will occur at different values of \(\theta\). For example, \(\frac{1}{2}(1+\cos \theta)\) will be \(1\) when \(\theta = \dotsc ,-4\pi, -2\pi, 0, 2\pi,4\pi, \dotsc\) (i.e. at even multiples of \(\pi\)) whereas \(\frac{1}{2}(1-\cos \theta)\) will be \(1\) when \(\theta = \dotsc,-5\pi, -3\pi, -\pi, \pi, 3\pi,5\pi, \dotsc\) (i.e. at odd multiples of \(\pi\)).
The right-hand side of each identity only involves \(\cos \theta\) and constants, so the graphs of \(y=\cos^2 \frac{\theta}{2}\) and \(y=\sin^2 \frac{\theta}{2}\) can be thought of as transformations of a \(y=\cos \theta\) graph. Which transformations are involved in each case? What is the frequency of \(y=\cos^2 \frac{\theta}{2}\) and \(y=\sin^2 \frac{\theta}{2}\)?
Again, from the right-hand side, the identities tell us that \(\cos^2 \frac{\theta}{2}\) is the mean of \(1\) and \(\cos \theta\) and \(\sin^2 \frac{\theta}{2}\) is the mean of \(1\) and \(-\cos \theta\). What does this tell you about the graph of \(y= \cos^2 \frac{\theta}{2}\) in relation to the graphs of \(y=1\) and \(y=\cos \theta\)?