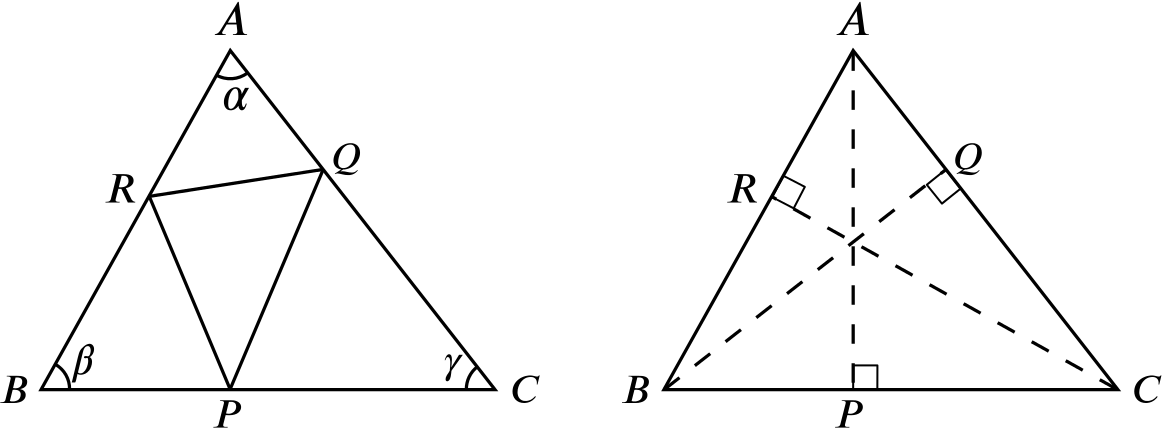
A triangle \(ABC\) has sides \(BC\), \(CA\), and \(AB\) of lengths \(a\), \(b\) and \(c\) respectively, and angles at \(A\), \(B\) and \(C\) are \(\alpha\), \(\beta\) and \(\gamma\) where \(0 \leq \alpha ,\beta ,\gamma \leq \frac{1}{2}\pi\).
Show that the area of \(ABC\) equals \(\frac{1}{2}bc\sin\alpha\).
Deduce the sine rule \[\frac{a}{\sin\alpha} = \frac{b}{\sin\beta} = \frac{c}{\sin\gamma}.\]
The points \(P\), \(Q\) and \(R\) are respectively the feet of the perpendiculars from \(A\) to \(BC\), \(B\) to \(CA\), and \(C\) to \(AB\) as shown.
Prove that \[\text{Area of $PQR$} = (1 - \cos^2 \alpha - \cos^2 \beta - \cos^2 \gamma) \times (\text{Area of $ABC$}).\]
For what triangles \(ABC\), with angles \(\alpha\), \(\beta\), \(\gamma\) as above, does the equation \[\cos^2 \alpha + \cos^2 \beta + \cos^2 \gamma =1\] hold?

