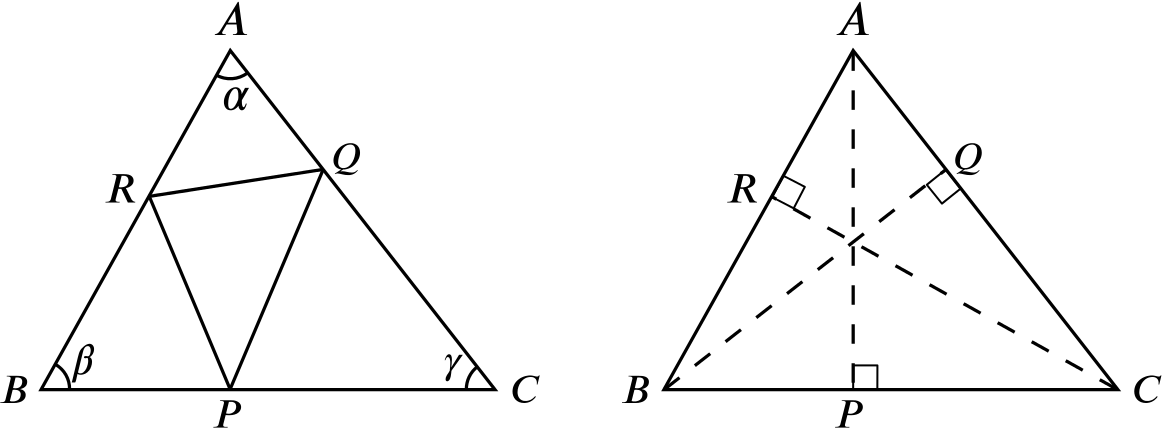
A triangle \(ABC\) has sides \(BC\), \(CA\), and \(AB\) of sides \(a\), \(b\) and \(c\) respectively, and angles at \(A\), \(B\) and \(C\) are \(\alpha\), \(\beta\) and \(\gamma\) where \(0 \leq \alpha ,\beta ,\gamma \leq \frac{1}{2}\pi\).
- Show that the area of \(ABC\) equals \(\frac{1}{2}bc\sin\alpha\).
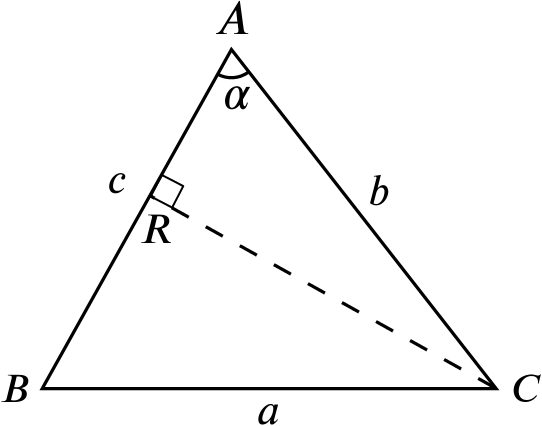
We take \(AB\) as the base, which has length \(c\), and \(CR\) as the height, which has length \(AC \sin(\angle CAR) = b \sin\alpha\). Then the triangle has area \[\frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2}cb \sin\alpha.\]
Deduce the sine rule \[\frac{a}{\sin\alpha} = \frac{b}{\sin\beta} = \frac{c}{\sin\gamma}.\]
By choosing a different side as the base of the triangle and using the same method, we see that the area is also given by \[\text{Area}(ABC) = \frac{1}{2}bc\sin\alpha = \frac{1}{2}ac\sin\beta = \frac{1}{2}ab\sin\gamma.\] If we divide through by \(\frac{1}{2}abc\), and then take the reciprocals of the equations, we get the sine rule \[\frac{a}{\sin\alpha} = \frac{b}{\sin\beta} = \frac{c}{\sin\gamma}.\]
- The points \(P\), \(Q\) and \(R\) are respectively the feet of the perpendiculars from \(A\) to \(BC\), \(B\) to \(CA\), and \(C\) to \(AB\) as shown.
Prove that \[\text{Area of $PQR$} = (1 - \cos^2 \alpha - \cos^2 \beta - \cos^2 \gamma) \times (\text{Area of $ABC$}).\]
It’s going to become very tedious writing the word “area” repeatedly in our equations. So we’ll use the notation \([ABC]\) to mean the area of triangle \(ABC\).

We have \([PQR]=[ABC]-[AQR]-[BRP]-[CPQ].\)
Consider the triangle \(AQR\). Using our formula from the first part, we have \[[AQR] = \frac{1}{2}AQ \times AR\times\sin\alpha.\] But we know \([ABC]=\dfrac{1}{2}bc\sin\alpha\), and so \[\sin \alpha = 2\dfrac{[ABC]}{bc}.\] Substituting, we get \[[AQR] = \frac{AQ \times AR}{b \times c} \times [ABC].\]
But if we look at the right-angled triangles \(RAC\) and \(BAQ\), we see that \[\cos\alpha = \dfrac{AR}{b}=\dfrac{AQ}{c},\]
and substituting gives \[[AQR] = \cos^2\alpha \times [ABC].\]
Similarly, \[[BPR] = \cos^2\beta \times [ABC],\] and \[[CQP] = \cos^2\gamma \times [ABC].\]
So finally \[\begin{align*} {}[PQR] &{}= [ABC] - [AQR] - [BPR] - [CQP]\\ &{}= (1 - \cos^2\alpha - \cos^2\beta - \cos^2\gamma) \times [ABC]. \end{align*}\]- For what triangles \(ABC\), with angles \(\alpha , \beta , \gamma\) as above, does the equation \[\cos^2 \alpha + \cos^2 \beta + \cos^2 \gamma =1\] hold?
If \(\cos^2 \alpha + \cos^2 \beta + \cos^2 \gamma =1\), then the area of the triangle \(PQR\) is zero.
This can only happen when two of \(P\), \(Q\) and \(R\) coincide - at the right angle of the triangle.
So this equation holds only if the triangle \(ABC\) is right-angled.
In fact, it is easy to see that we have an if and only if relationship here: \(\cos^2 \alpha + \cos^2 \beta + \cos^2 \gamma =1\) if and only if the triangle \(ABC\) is right-angled.

