We take a circle and inscribe a triangle in it.
Complete the steps of the table below to find an interesting relationship between the angles and sides of this triangle.
| Diagram | Description |
|---|---|
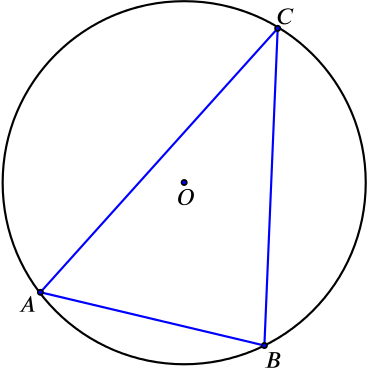
|
1. Add a point \(C'\) on the circumference of the circle, so that \(\angle C'AB\) is a right-angle. 2. What is the relationship between angles \(ACB\) and \(AC'B\)? 3. What is the length \(C'B\)? |

|
4. Label side \(AB\) as \(c\). Write a relationship between \(c\) and the angle at \(C'\). |

|
5. Can you therefore write a relationship between \(c\) and the angle at \(C\)? |

|
6. Starting from the original diagram, add a point \(B'\) on the circumference of the circle, so that \(\angle B'CA\) is a right-angle. 7. What is the relationship between angles \(ABC\) and \(AB'C\)? 8. What is the length \(B'A\)? |

|
9. Label side \(AC\) as \(b\). Write a relationship between \(b\) and the angle at \(B'\). |

|
10. Therefore write a relationship between \(b\) and the angle at \(B\). |

|
11. In general, what can we now say about the relationship between the sides and angles of a triangle? |
You have proved your statement for this particular triangle, which has its three vertices on the circumference of a circle. Is your statement true for all triangles?
If you are not sure, you might like to look at Finding circles.

