| Diagram | Description |
|---|---|
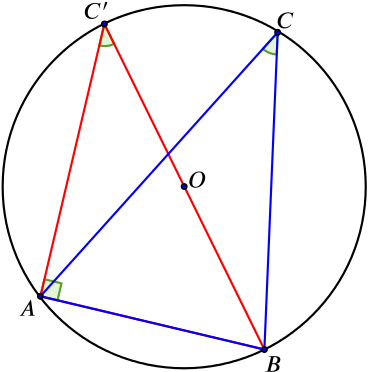
|
1. Add a point \(C'\) on the circumference of the circle, so that \(\angle C'AB\) is a right-angle. 2. What is the relationship between angles \(ACB\) and \(AC'B\)? \(\color{blue}{\angle AC'B = \angle ACB}\) \(\color{blue}{\text{as they are angles on the circumference}}\) \(\color{blue}{\text{subtended by the same arc.}}\) 3. What is the length \(C'B\)? \(\color{blue}{C'B = 2R}\) \(\color{blue}{\text{where }R = \text{radius}.}\) |
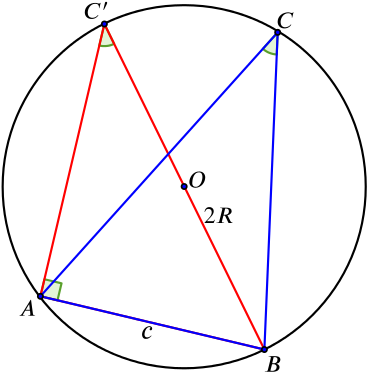
|
4. Label side \(AB\) as \(c\). Write a relationship between \(c\) and \(C'\). \(\color{blue}{\sin{C'} = \dfrac{c}{2R}}\) |

|
5. Can you therefore write a relationship between \(c\) and the angle at \(C\)? \(\color{blue}{\text{As $C = C'$ and $\sin{C'} = \dfrac{c}{2r}$,}}\) \(\color{blue}{\text{then}}\) \(\color{blue}{\sin{C} = \dfrac{c}{2R}}\). |
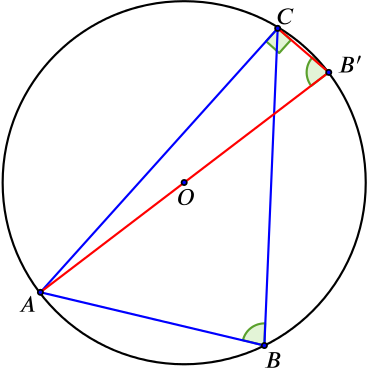
|
6. Starting from the original diagram, can you add a point \(B'\) on the circumference of the circle, so that \(\angle B'CA\) is a right-angle? 7. What is the relationship between angles \(ABC\) and \(AB'C\)? \(\color{blue}{\angle CB'A = \angle CBA}\) \(\color{blue}{\text{as before.}}\) 8. What is the length of \(B'A\)? \(\color{blue}{B'A = 2R}\) |
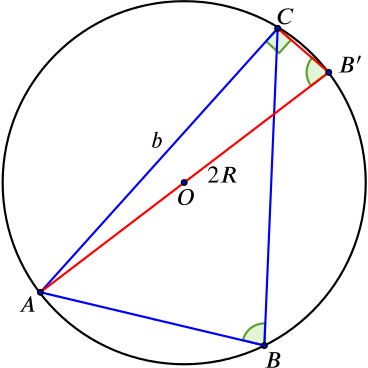
|
9. Label side \(AC\) as \(b\). Write a relationship between \(b\) and the angle at \(B'\). \(\color{blue}{\sin{B'} = \dfrac{b}{2R}}\) 10. Therefore write a relationship between \(b\) and the angle at \(B\). \(\color{blue}{\text{As $B = B'$ and $\sin{B'} = \dfrac{b}{2R}$,}}\) \(\color{blue}{\text{then}}\) \(\color{blue}{\sin{B} = \dfrac{b}{2R}.}\) |
If we did this for a third time, for point \(A\), then we would get
\[\sin{A} = \dfrac{a}{2R}.\]
Did you notice that we didn’t even need to do this for a second time with point \(B\)? We could have chosen to label our triangle in any way we like, so our reasoning from steps one to five is symmetrical for points \(C\), \(B\) and \(A\).
So we now have three statements linking the side of a triangle with its opposite angle:
\[\sin{A} = \dfrac{a}{2R},\] \[\sin{B} = \dfrac{b}{2R},\] \[\sin{C} = \dfrac{c}{2R}.\]
Rearranging these gives us
\[2R = \dfrac{a}{\sin{A}}=\dfrac{b}{\sin{B}}=\dfrac{c}{\sin{C}}.\]
You are probably familiar with most of this statement, and see that we have proved the sine rule. However, the fact that this common ratio also equals \(2r\) may be unfamiliar.
We have uncovered the relationship, \[2R = \dfrac{a}{\sin{A}}=\dfrac{b}{\sin{B}}=\dfrac{c}{\sin{C}},\] where \(r\) is the radius of the circle that passes through the vertices of the triangle.
This relationship is true for all triangles, as we can always draw a circle through the three vertices of a triangle. This is called the circumcircle of the triangle, and its centre is known as the circumcentre of the triangle. This is one of many different ways to define the centre of a triangle.
In addition to this, if we begin with a fixed circle, then any triangle we inscribe within it will have the property that \(\dfrac{a}{\sin A}=\dotsb=2R\), a fixed number! So this relationship is invariant: it holds for all such triangles, regardless of their side lengths or angles, as long as it remains inscribed in our fixed circle.

