This diagram shows the ellipse with equation \(x^2+4y^2=16\) together with the straight line \(y=x+c\).
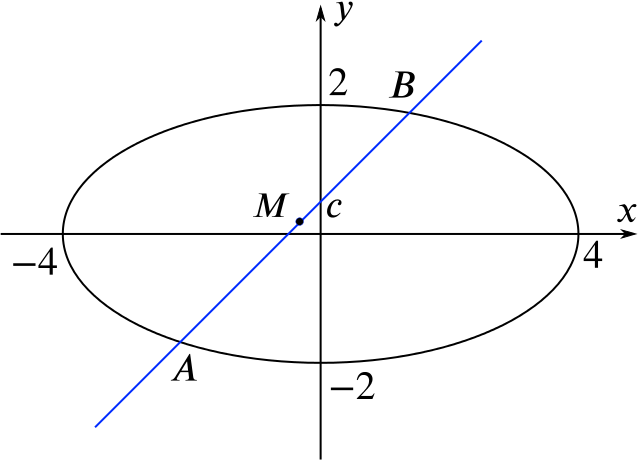
The line and ellipse intersect at the points \(A\) and \(B\), and the midpoint of \(AB\) is \(M\).
Find the coordinates of \(M\) for some different values of \(c\).
What do you notice?
What would happen if you used straight lines of a different gradient instead?

