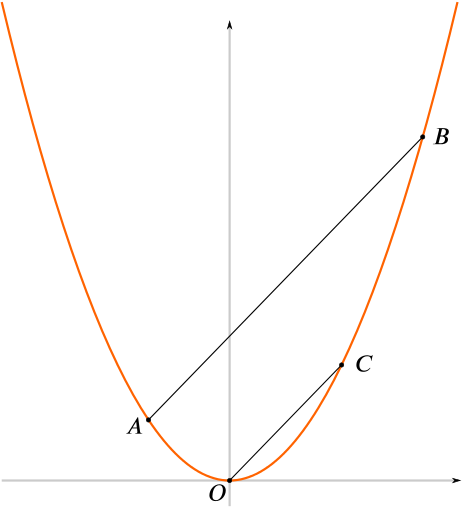
Take any two points \(A\) and \(B\) on the parabola \(y = x^2\).
Draw the line \(OC\) through the origin, parallel to \(AB\), cutting the parabola again at \(C\).
Let \(A\) have coordinates \((a,a^2)\), let \(B\) have coordinates \((b,b^2)\) and let \(C\) have coordinates \((c,c^2)\).
Prove that \(a+b = c\).
Imagine drawing another parallel line \(DE\), where \(D\) and \(E\) are two other points on the parabola. Extend the ideas of the previous result to prove that the midpoints of each of the three parallel lines lie on a straight line.

