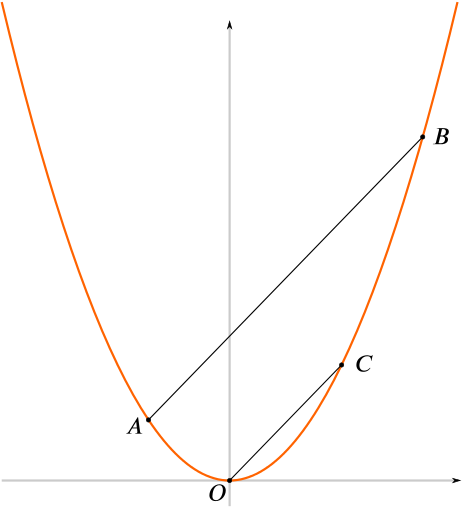
Take any two points \(A\) and \(B\) on the parabola \(y = x^2\).
Draw the line \(OC\) through the origin, parallel to \(AB\), cutting the parabola again at \(C\).
Let \(A\) have coordinates \((a,a^2)\), let \(B\) have coordinates \((b,b^2)\) and let \(C\) have coordinates \((c,c^2)\).
Prove that \(a+b = c\).
We know that
\(A=(a,a^2)\),
\(B=(b,b^2)\),
\(C=(c,c^2)\).
We can calculate the gradient of a straight line between two points \((x_1,y_1)\) and \((x_2,y_2)\) as \(\frac{y_1-y_2}{x_1-x_2}\).
So the gradient of line \(AB\) is equal to \(\frac{a^2-b^2}{a-b}=a+b\).
Also, the gradient of line \(OC\) is equal to \(\frac{0-c^2}{0-c}=c\).
However, we know from the question that these two lines are parallel. Two lines are parallel if and only if they have the same gradient, which means that we must have \(a+b=c\).
Imagine drawing another parallel line \(DE\), where \(D\) and \(E\) are two other points on the parabola. Extend the ideas of the previous result to prove that the midpoints of each of the three parallel lines lie on a straight line.
Now, suppose that we have two points \(D=(d,d^2)\) and \(E=(e,e^2)\) on the parabola making another line parallel to \(OC\).
The gradient of line \(DE\) is equal to \(\frac{d^2-e^2}{d-e}=d+e\). As \(DE\) is parallel to \(OC\), we also have \(d+e=c\).
We can calculate the midpoint of a straight line between two points \((x_1,y_1)\) and \((x_2,y_2)\) as \((\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})\).
So the midpoint of line \(OC\) is \[\left(\frac{0+c}{2},\frac{0+c^2}{2}\right) = \left(\frac{c}{2},\frac{c^2}{2}\right).\]
The midpoint of line \(AB\) is \[\left(\frac{a+b}{2},\frac{a^2+b^2}{2}\right) = \left(\frac{c}{2},\frac{a^2+b^2}{2}\right).\]
The midpoint of line \(DE\) is \[\left(\frac{d+e}{2},\frac{d^2+e^2}{2}\right) = \left(\frac{c}{2},\frac{d^2+e^2}{2}\right).\]
All three of these points have an \(x\)-coordinate of \(\frac{c}{2}\). This means that the line \(x=\frac{c}{2}\) passes through the midpoints of the lines \(OC\), \(AB\) and \(DE\).

