This diagram shows the ellipse with equation \(x^2+4y^2=16\) together with the straight line \(y=x+c\).
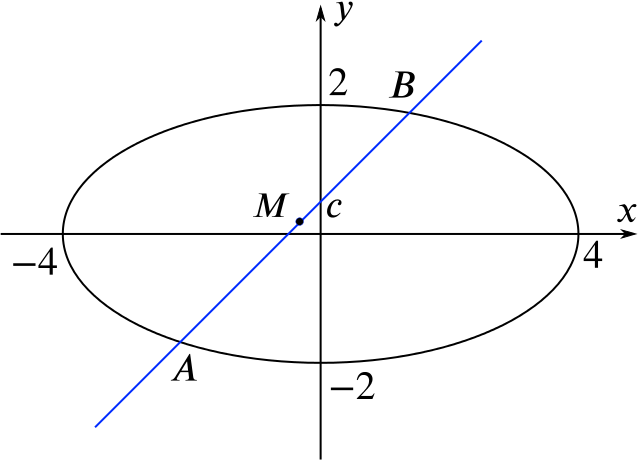
The line and ellipse intersect at the points \(A\) and \(B\), and the midpoint of \(AB\) is \(M\).
Find the coordinates of \(M\) for some different values of \(c\).
Let’s say we begin by considering the case where \(c=1\), so we have the two equations \(x^2+4y^2=16\) and \(y=x+1\).
Before we continue, let’s just stop and think. Why did we choose \(c=1\)?
- What does the case where \(c=1\) look like in the diagram?
- What other values of \(c\) could we have chosen?
- Are there any values of \(c\) that you would not choose? Why?
We can use the formula to find the solutions of this quadratic: they are \[x=\frac{-8\pm\sqrt{8^2+4\times5\times12}}{10}.\] We could simplify this, but instead we notice that these two solutions are the \(x\)-coordinates of \(A\) and \(B\). As the \(x\)-coordinate of \(M\) is the mean of these, we only need to add them together and halve the answer. When we add the two solutions together, the square roots cancel and we are left with \(\frac{-8}{10}+\frac{-8}{10}\). So the \(x\)-coordinate of \(M\) is half of this, which is \(\frac{-8}{10}=-\frac{4}{5}\).
Since \(M\) lies on the straight line \(y=x+1\), it follows that the \(y\)-coordinate of \(M\) is \(-\frac{4}{5}+1=\frac{1}{5}\). Hence \(M\) has coordinates \(\bigl(-\frac{4}{5}, \frac{1}{5}\bigr)\).
We could have been even more sneaky in saving work for ourselves!
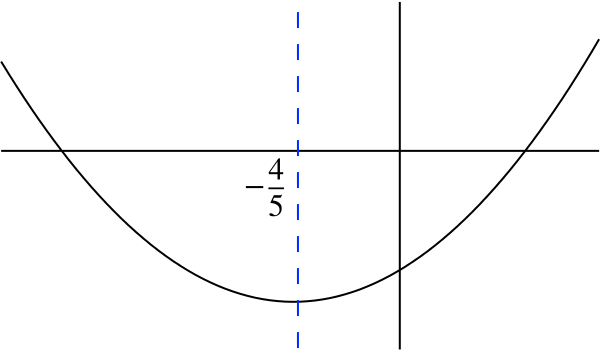
If we begin to complete the square for the quadratic in equation \(\eqref{eq:eg}\), we have \[5x^2+8x-12=5\bigl(x^2+\tfrac{8}{5}x\bigr)-12=5\bigl(x+\tfrac{4}{5}\bigr)^2+k\] for some number \(k\). The graph \(y=5x^2+8x-12\) therefore has a line of symmetry \(x=-\frac{4}{5}\) and so the two solutions are symmetrically placed about this \(x\)-value, as shown in this sketch. It follows that their mean is \(-\frac{4}{5}\).
And we could do this algebraically, too. If we write \[5x^2+8x-12=5(x-\alpha)(x-\beta)=5(x^2-(\alpha+\beta)x+\alpha\beta),\] where the solutions (or roots) of the quadratic are \(\alpha\) and \(\beta\), then we see that \(-5(\alpha+\beta)=8\), so the sum of the roots is \(-\frac85\), and their mean is \(-\frac45\).
In the example above, we used \(c=1\) and found that \(M\) had coordinates \(\bigl(-\tfrac{4}{5},\tfrac{1}{5}\bigr)\). When you use other values of \(c\), you may find that the coordinates are also quite simple. There does seem to be an interesting pattern to the coordinates: what happens if you plot them?
What is the locus of \(M\)?
What would happen if you used straight lines of a different gradient instead?
What is the locus of \(M\) in these cases?
Can you find a relation between the gradient of the straight lines and the locus of \(M\)?
This problem considered an ellipse. You might find it interesting to compare this with your answer to Parabella. You could also try answering the same question for a hyperbola such as \(x^2-4y^2=16\), which is the other type of conic section. Does that also give a similar answer? If so, why, and if not, why not?

