What do you do when you are lost? If you are lucky enough to have a smart phone, you’ll probably use the GPS feature. This pin-points your global coordinates using information sent from satellites (see Conic sections in real life). But what are those global coordinates?
Ordinary flat maps are often divided up into a grid formed by vertical and horizontal lines. The resulting grid boxes are usually labelled by letters (A, B, C, etc.) in the horizontal direction, and by numbers (1,2,3, etc.) in the vertical direction. To find a location, say a particular street in your home town, you look up its coordinates, for example A4, in the index, and then find the grid box labelled by that letter and number. The street you are looking for will be within this box.
Navigation around the spherical Earth uses the same idea, only here the grid isn’t formed by straight lines but by circles that lie on the surface of the Earth. One set of circles (which we can think of as horizontal) comes from planes that are perpendicular to the rotation axis of the Earth. These slice right through the Earth, meeting its surface in circles which are called lines of latitude. The radii of these circles vary: the largest one is the equator, which chops the Earth neatly into northern and southern hemispheres. As you move north or south the circles become smaller, and at the poles they are just points.
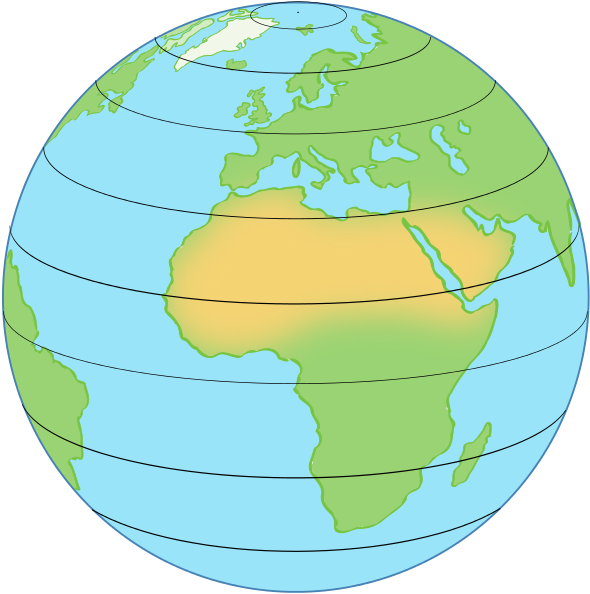
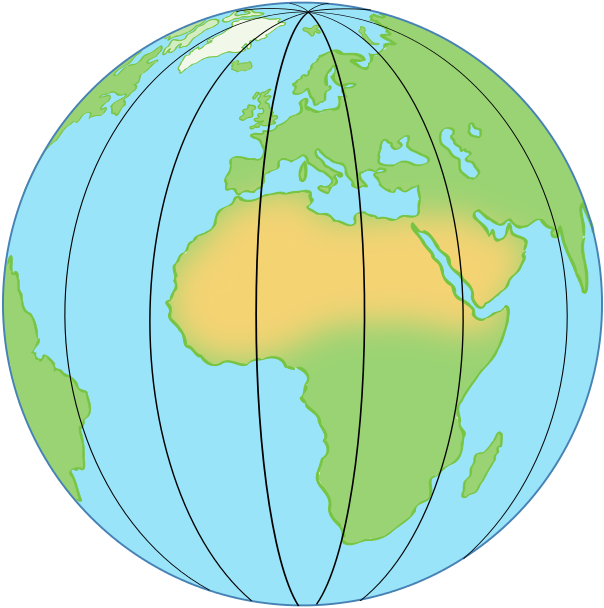
The other set of circles (which we can think of as the vertical lines) come from planes that slice right through the Earth and contain the axis around which it rotates. Such planes meet the surface of the Earth in circles that contain both poles, are centred on the same point as the Earth itself and have the same radius as the Earth. One half of such a circle, running from the north pole to the south pole, is called a line of longitude or a meridian (one famous example is the Greenwich meridian).
Lines of latitude and longitude are labelled by angles. Imagine a particular line of latitude, pick a point \(p\) on it, and draw a line from \(p\) to the centre of the Earth. Now measure the angle \(\phi\) that this line makes with the plane containing the equator—it is the same no matter what point \(p\) on the line of latitude you picked.
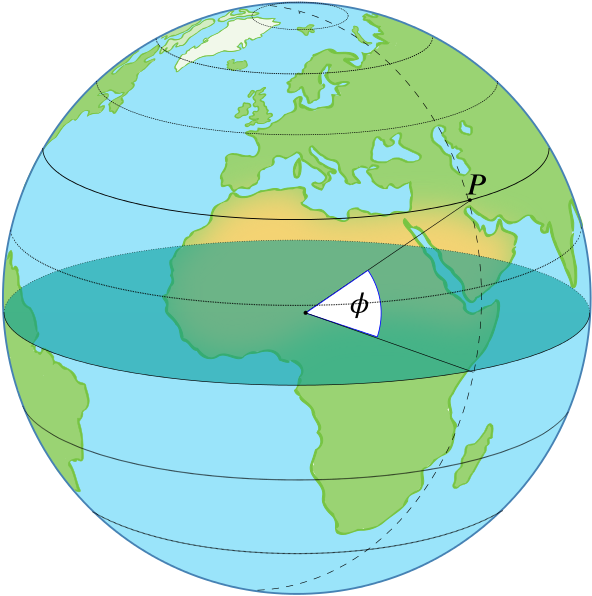
If you are on the equator, then \(\phi = 0^{\circ}\), and if you are right on the north or south pole, then \(\phi = 90^{\circ}\). To distinguish between the northern and southern hemispheres, people often write \(\phi\) N (for the former) or \(\phi\) S (for the latter).
The angle of a line of longitude is measured with respect to a very special meridian: the one that runs from the north pole to the south pole and passes through Greenwich, in south London (that’s a historical accident —see The longitude problem). The angle \(\lambda\) defining another meridian is the angle through which you would have to rotate that meridian around the rotation axis of the Earth to make it coincide with the Greenwich meridian.
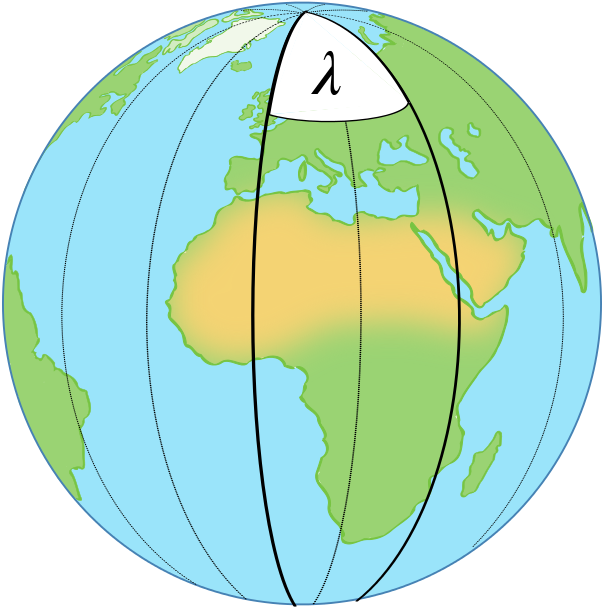
The Greenwich meridian itself has longitude \(\lambda = 0^{\circ}\). The \(180^{\circ}\) meridian is the other half of the great circle containing the Greenwich meridian. It passes through Russia, the Pacific ocean and Fiji, and it’s the international date line: cross it and you travel one day into the past or future. For any longitude \(\lambda\) other than \(0^{\circ}\) and \(180^{\circ}\), people often write \(\lambda\) W to indicate a location between the Greenwich meridian and the \(180^\circ\) meridian and west of the former, and \(\lambda\) E to indicate a location between the Greenwich meridian and the \(180^\circ\) meridian and east of the former.
By picking a certain set of latitude and longitude lines we can create a grid that chops the Earth into regions, just as a street map is chopped into squares. But we can pin-point our location more precisely. Wherever you are on Earth, you will always be sitting at the crossing point of one particular line of latitude and one particular line of longitude. The corresponding angles describe exactly where you are. For example, the global coordinates of Greenwich are \(51.48^{\circ}\) N, \(0^{\circ}\) W (where latitude is given first). The coordinates of the Empire State Building in New York are \(40.7484^{\circ}\) N, \(73.9857^{\circ}\) W. And the coordinates of the Sydney Opera House are \(33.8587^{\circ}\) S, \(151.2140^{\circ}\) E.
But hang on a second. This gives you a way of finding a particular place on Earth. But how are you supposed to work out your coordinates in the first place, for example when you are lost at sea with your smart phone run out of battery? Find out more in Calculating latitude and The longitude problem.

