We are still along the same stretch of road, with a speed limit of \(\quantity{50}{mph}\), and the average speed cameras set at \(\quantity{4}{miles}\) apart. In this instance our first driver spends the same amount of time driving at \(\quantity{46}{mph}\) as he does at \(\quantity{62}{mph}\). Our second driver drives the first half of the distance at \(\quantity{46}{mph}\) and the second half at \(\quantity{62}{mph}\).
What are the average speeds of each driver? Will either of them be caught speeding?
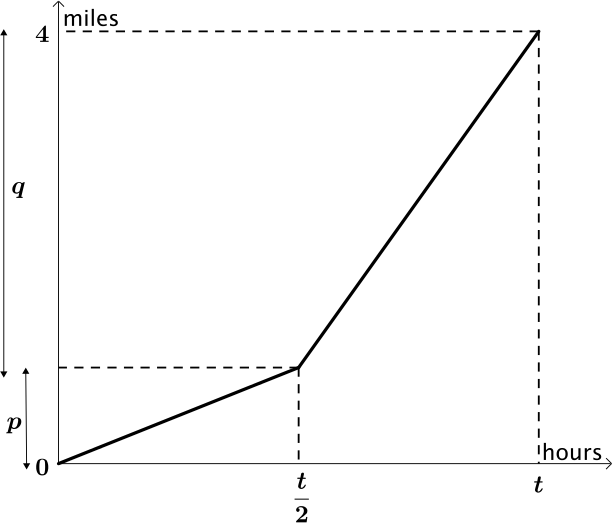
Let’s start with the first driver, who travels half the time at \(\quantity{46}{mph}\) and half the time at \(\quantity{62}{mph}\). This is represented by the graph above.
We have two different ways to think about the journey; as a whole, and split into its two pieces.
We can write the speeds of the two pieces as \[46=\dfrac{p}{\frac{1}{2}t}\quad\text{and}\quad 62 = \dfrac{q}{\frac{1}{2}t},\] where \(p\) and \(q\) are the distances travelled.
The journey as a whole can be written as \[ \text{average speed} = \dfrac{p+q}{t}.\]
We know that \(p+q = 4\) but it turns out that substituting this into the equation is not helpful.
Therefore we can substitute in values for \(p\) and \(q\) in terms of \(t\), \[ \textrm{ average speed } = \dfrac{23t+31t}{t},\] which leaves us with an average speed of \(\quantity{54}{mph}\).
What do you notice about the average speed? Could you have reasoned through this answer more easily, without doing the calculations?
Now we come to the driver who travels half the distance at each speed. Again we can think about the parts of the journey and the journey as a whole.
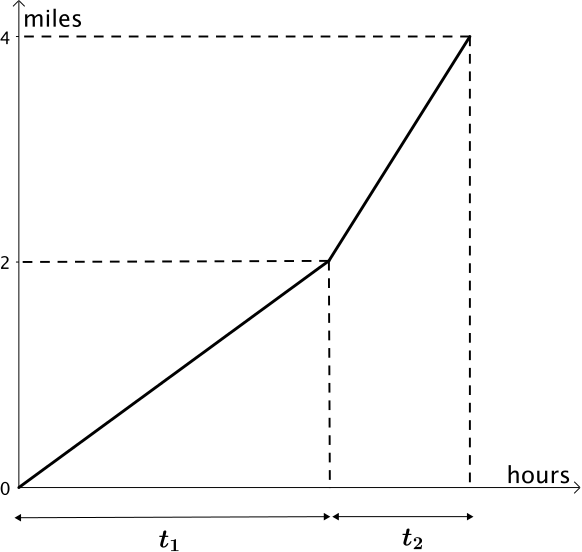
The separate parts can be written \[46 = \dfrac{2}{t_1} \quad \textrm{and} \quad 62 = \dfrac{2}{t_2}.\]
Will they spend a longer time travelling at \(\quantity{46}{mph}\) or at \(\quantity{62}{mph}\)?
The whole journey gives us
\[\text{average speed}=\dfrac{4}{t_1+t_2}.\]
Rearranging the above equations to find \(t_1\) and \(t_2\) and then substituting these in gives
\[\text{average speed}=\dfrac{4}{\dfrac{2}{46}+\dfrac{2}{62}}= \quantity{52.8}{mph}\ \text{($3$ sf)}.\]
Do you think that either driver will be given a speeding ticket?
What happens if the speed cameras are \(\quantity{10}{miles}\) apart instead? What changes?
Did you find that anything changed as the distance increased? Does this surprise you? Can you prove your findings for any distance?

