In the diagram below, \(P\) is a point on a circle of radius \(1\) and \(\theta\) is the angle between \(OP\) and the positive \(x\)-axis.
We have drawn in the diameter through \(P.\)
- \(M\) is the point where the diameter through \(P\) meets the line \(x=1\)
- \(N\) is the point where the diameter through \(P\) meets the line \(y=1\)
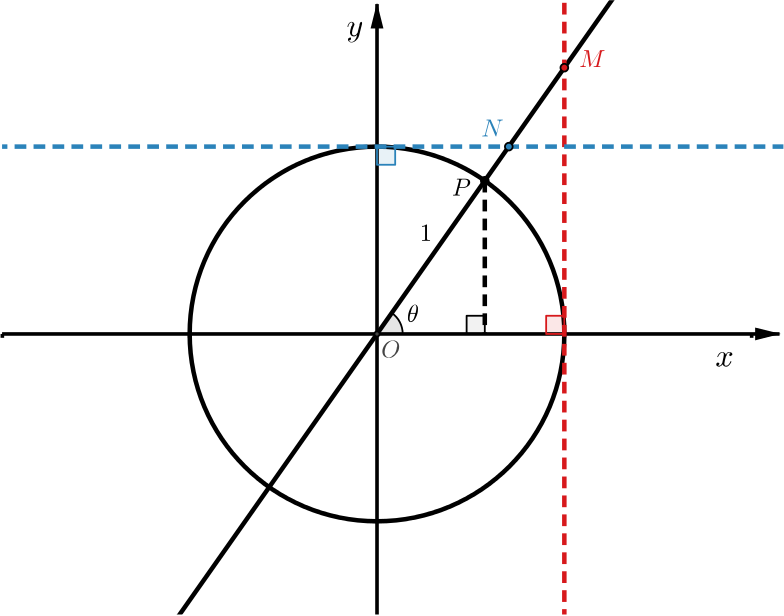
Using the functions from the triangles problem, work out the coordinates of points \(P\), \(M\) and \(N.\)
The triangles in the previous part of the problem may help you to work out some side lengths.
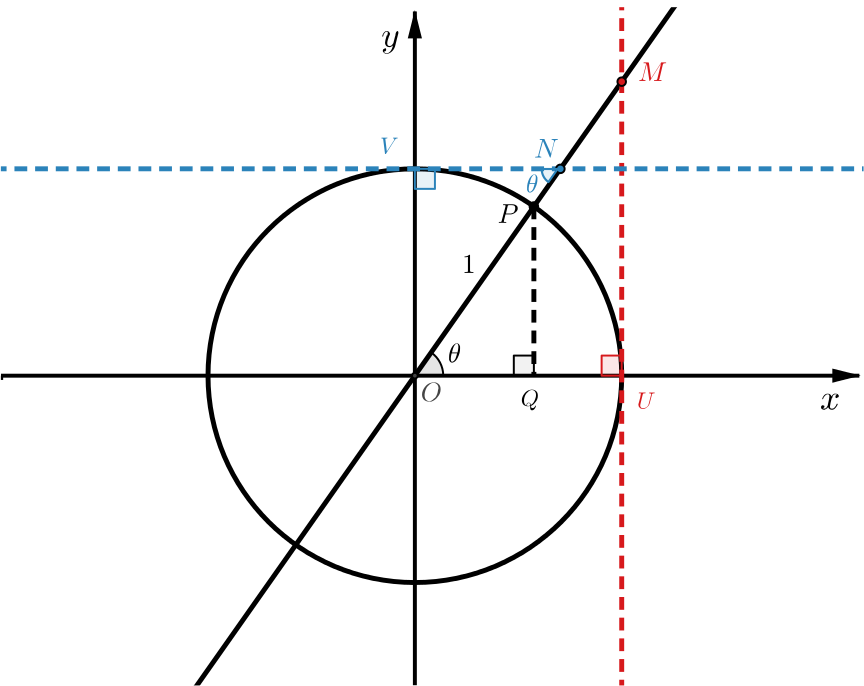
We have added some extra labels to the diagram.
The hypotenuse of \(OPQ\) has length \(1\), so \(OQ\) has length \(\cos \theta\) and \(QP\) has length \(\sin \theta\). This means that the coordinates of \(P\) are \((\cos \theta, \sin \theta)\).
To find the \(y\)-coordinate of \(M\), note that \(OU\) has length \(1\) so \(UM\) has length \(\tan \theta\). Therefore \(M\) has coordinates \((1, \tan \theta)\). The similarity of triangles \(OPQ\) and \(OMU\) again tells us that \(\tan \theta = \dfrac{\sin \theta}{\cos \theta}\).
To find the \(x\)-coordinate of \(N\), note that \(y=1\) is parallel to the \(x\)-axis so angle \(ONV\) is \(\theta.\) As \(OV\) has length \(1\), this means the coordinates of \(N\) are \((\cot \theta, 1)\).
As \(\theta\) varies, how will \(M\) and \(N\) move? What happens when \(\theta\) isn’t acute?
- When will \(M\) and \(N\) be moving quickly?
- Do \(M\) and \(N\) always move smoothly?
- When will their \(x\)- or \(y\)-coordinates change sign?
You can see how \(M\) and \(N\) move as \(\theta\) varies in the GeoGebra file below.
Could you sketch graphs of \(\tan \theta\) against \(\theta\) and \(\cot \theta\) against \(\theta\)? Download this file to see the graph of \(y=\tan \theta\) traced out.
In the next diagram, we have drawn the tangent to the circle at \(P\) and marked the points where the tangent at \(P\) meets the axes.
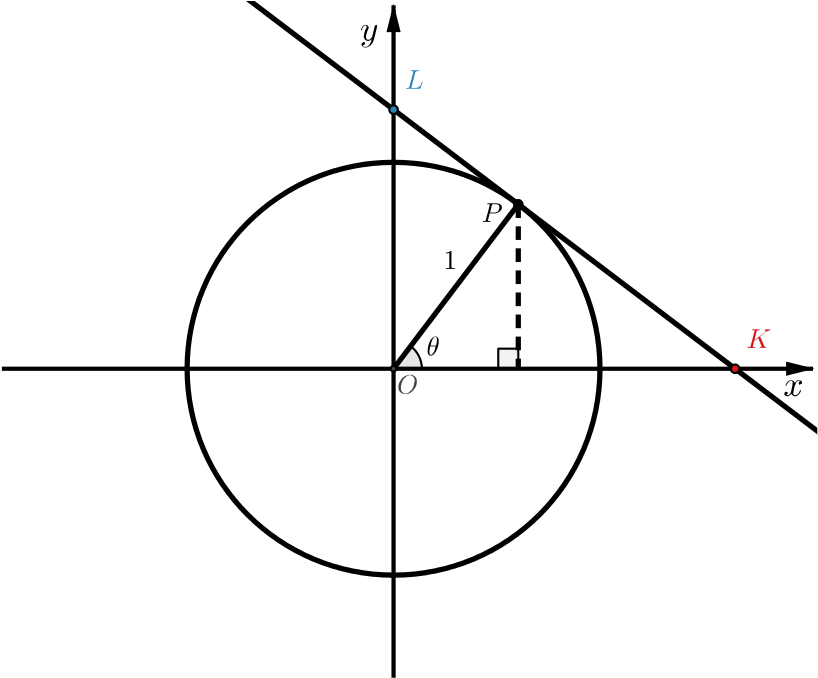
What are the coordinates of \(K\) and \(L\)? How will \(K\) and \(L\) move along the axes as \(\theta\) varies?
The line \(LK\) is a tangent to the circle at \(P\), so \(OP\) is at right angles to \(LK\).
Therefore triangle \(OPK\) is right-angled with angle \(\theta\) at \(O\) and adjacent side of length \(1\). This means that \(OK\) has length \(\sec \theta\) and the coordinates of \(K\) are \((\sec \theta, 0)\).
Likewise, triangle \(OPL\) is right-angled with angle \(\theta\) at \(L\), so \(L\) has coordinates \((0,\cosec \theta)\).
You can see how \(K\) and \(L\) move as \(\theta\) varies in the GeoGebra file below. Could you sketch graphs of \(\sec \theta\) and \(\cosec \theta\) against \(\theta\)?
We have used \(\theta\) to parametrise the circle because as \(\theta\) varies, the locus of the point \(P(\cos \theta, \sin \theta)\) is a circle, centre \(0\), radius \(1.\) We could say that \(\theta\) parametrises the lines \(x=1\) and \(y=1\) because the points \(M(1, \tan \theta)\) and \(N(\cot \theta,1)\) trace out these lines as \(\theta\) varies. Similarly, we could say that the \(x\) and \(y\) axes are parametrised by \(\theta\) via the points \(K(\sec \theta,0)\) and \(L(0, \cosec \theta)\) respectively.

