The trigonometric functions with which we are most familiar are sine and cosine. From them, we can obtain tangent, and also the reciprocals secant, cosecant and cotangent. In the past, mathematicians have used many other trigonometric functions too. Some of these are illustrated below. (You can read more about the history and use of these in navigation in Lost but lovely: the haversine.)
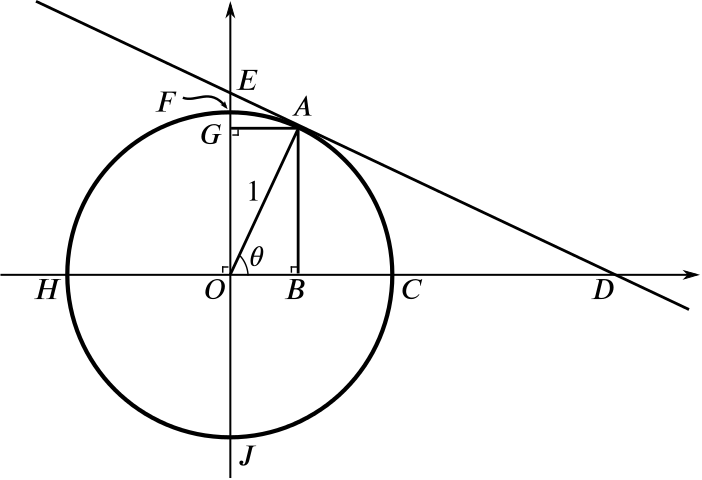
Find the following lengths, in terms of \(\sin\theta\) and \(\cos \theta\).
\(OB\)
\(AB\)
\(BC\) (this was known as the versed sine or versine of \(\theta\), written \(\mathop{\mathrm{versin}}\theta\))
\(OD\)
\(CD\) (this was known as the exsecant of \(\theta\), written \(\mathop{\mathrm{exsec}}\theta\))
\(AD\)
\(AE\)
\(AG\)
\(GO\)
\(FG\) (this was known as the coversed sine or coversine of \(\theta\), written \(\mathop{\mathrm{coversin}}\theta\) or \(\mathop{\mathrm{covers}}\theta\) or \(\mathop{\mathrm{cvs}}\theta\))
\(EF\) (this was known as the excosecant of \(\theta\), written \(\mathop{\mathrm{excosec}}\theta\) or \(\mathop{\mathrm{excsc}}\theta\))
Can you find line segments on the diagram that have the following lengths?
The versed cosine or vercosine of \(\theta\), written as \(\mathop{\mathrm{vercos}}\theta\), which is defined by \[\mathop{\mathrm{vercos}}\theta = 1 + \cos\theta\]
The coversed cosine or covercosine of \(\theta\), written as \(\mathop{\mathrm{covercos}}\theta\), which is defined by \[\mathop{\mathrm{covercos}}\theta = 1 + \sin\theta\]
We know that \(\cos\theta = \sin\left(\frac{\pi}{2} - \theta\right)\).
How are versine and coversine related?
How are vercosine and covercosine related?
What do you think that the prefix “co-” might indicate here?

