The trigonometric functions with which we are most familiar are sine and cosine. From them, we can obtain tangent, and also the reciprocals secant, cosecant and cotangent. In the past, mathematicians have used many other trigonometric functions too. Some of these are illustrated below.
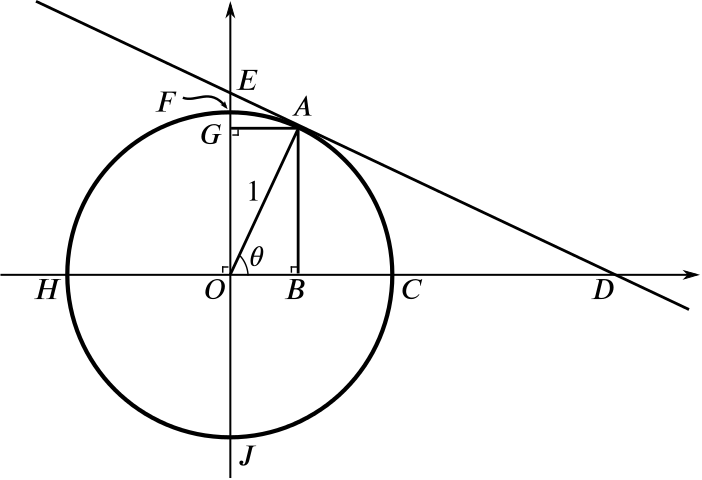
Find the following lengths, in terms of \(\sin\theta\) and \(\cos \theta\).
\(OB\)
\(AB\)
\(BC\) (this was known as the versed sine or versine of \(\theta\), written \(\mathop{\mathrm{versin}}\theta\))
The triangle \(OAB\) is right-angled, with a right angle at \(B\) and with hypotenuse of length \(1\), so we see that \[OB = \cos\theta.\]
Similarly, we have \(AB = \sin\theta.\)
Since the circle is a unit circle, we know that \(OC = 1\) and so \[BC = OC - OB = 1 - \cos \theta.\] This tells us that \(\mathop{\mathrm{versin}}\theta = 1 - \cos \theta.\)
\(OD\)
\(CD\) (this was known as the exsecant of \(\theta\), written \(\mathop{\mathrm{exsec}}\theta\))
The triangle \(OAD\) is right-angled, with a right angle at \(A\) and with \(\angle DOA = \theta\), and the side \(OA\) has length \(1\), so we find that \(\cos\theta = \dfrac{1}{OD},\) so \[OD = \dfrac{1}{\cos\theta}.\]
Therefore we have \[CD = OD-OC = \dfrac{1}{\cos\theta} - 1 = \sec\theta - 1.\] This means we can write \(\mathop{\mathrm{exsec}}\theta = \sec\theta - 1.\)
\(AD\)
\(AE\)
Looking again at triangle \(OAD\), we find that \[AD = \tan\theta = \dfrac{\sin\theta}{\cos\theta}.\]
We can consider triangle \(AOE\), which has a right angle at \(A\) and which has angle \(\theta\) at \(E\). The side \(AO\) has length \(1\), and so we see that \(\tan\theta = \dfrac{1}{AE},\) and therefore \[AE = \cot\theta = \dfrac{\cos\theta}{\sin\theta}.\]
\(AG\)
\(GO\)
\(FG\) (this was known as the coversed sine or coversine of \(\theta\), written \(\mathop{\mathrm{coversin}}\theta\) or \(\mathop{\mathrm{covers}}\theta\) or \(\mathop{\mathrm{cvs}}\theta\))
Triangle \(AGE\) has a right angle at \(G\) and angle \(\theta\) at \(E\), and we have just seen that its hypotenuse has length \(\cot\theta\). So \[AG = \cot\theta \sin\theta = \cos\theta.\]
Quadrilateral \(ABOG\) is a rectangle, because its angles are all right angles, so \[GO = AB = \sin\theta.\]
The circle has radius \(1\), so \[FG = FO - GO = 1 - \sin\theta.\] Therefore \(\mathop{\mathrm{coversin}}\theta = 1 - \sin\theta.\)
- \(EF\) (this was known as the excosecant of \(\theta\), written \(\mathop{\mathrm{excosec}}\theta\) or \(\mathop{\mathrm{excsc}}\theta\))
We can find the length \(EO\) using the right-angled triangle \(DOE\), which has an angle \(\theta\) (at \(E\)). We know that \(OD = \sec\theta\), and so we have \[EO = \dfrac{\sec\theta}{\tan\theta} = \dfrac{1}{\sin\theta}.\]
Then we have \[EF = EO - 1 = \dfrac{1}{\sin\theta} - 1.\] Therefore we can write \(\mathop{\mathrm{excosec}}\theta= \cosec \theta -1.\)
Can you find line segments on the diagram that have the following lengths?
The versed cosine or vercosine of \(\theta\), written as \(\mathop{\mathrm{vercos}}\theta\), which is defined by \[\mathop{\mathrm{vercos}}\theta = 1 + \cos\theta.\]
The coversed cosine or covercosine of \(\theta\), written as \(\mathop{\mathrm{covercos}}\theta\), which is defined by \[\mathop{\mathrm{covercos}}\theta = 1 + \sin\theta.\]
Since the circle has radius \(1\) and \(OB = \cos\theta\), the line segment \(BH\) has length \(1 + \cos\theta\).
Similarly, \(GJ\) has length \(1 + \sin\theta\).
We know that \(\cos\theta = \sin\left(\dfrac{\pi}{2} - \theta\right)\).
How are versine and coversine related?
How are vercosine and covercosine related?
- What do you think that the prefix “co-” might indicate here?
The prefix “co-” probably originates from the word “complementary”. Two angles are called complementary if they add up to a right angle. So:
the cosine of an angle is the sine of the complementary angle
the cosecant (cosec) of an angle is the secant (sec) of the complementary angle
the cotangent (cotan) of an angle is the tangent (tan) of the complementary angle
the coversine of an angle is the versine of the complementary angle
the covercosine of an angle is the vercosine of the complementary angle

