In the diagram below, \(P\) is a point on a circle of radius \(1\) and \(\theta\) is the angle between \(OP\) and the positive \(x\)-axis.
We have drawn in the diameter through \(P.\)
- \(M\) is the point where the diameter through \(P\) meets the line \(x=1\)
- \(N\) is the point where the diameter through \(P\) meets the line \(y=1\)
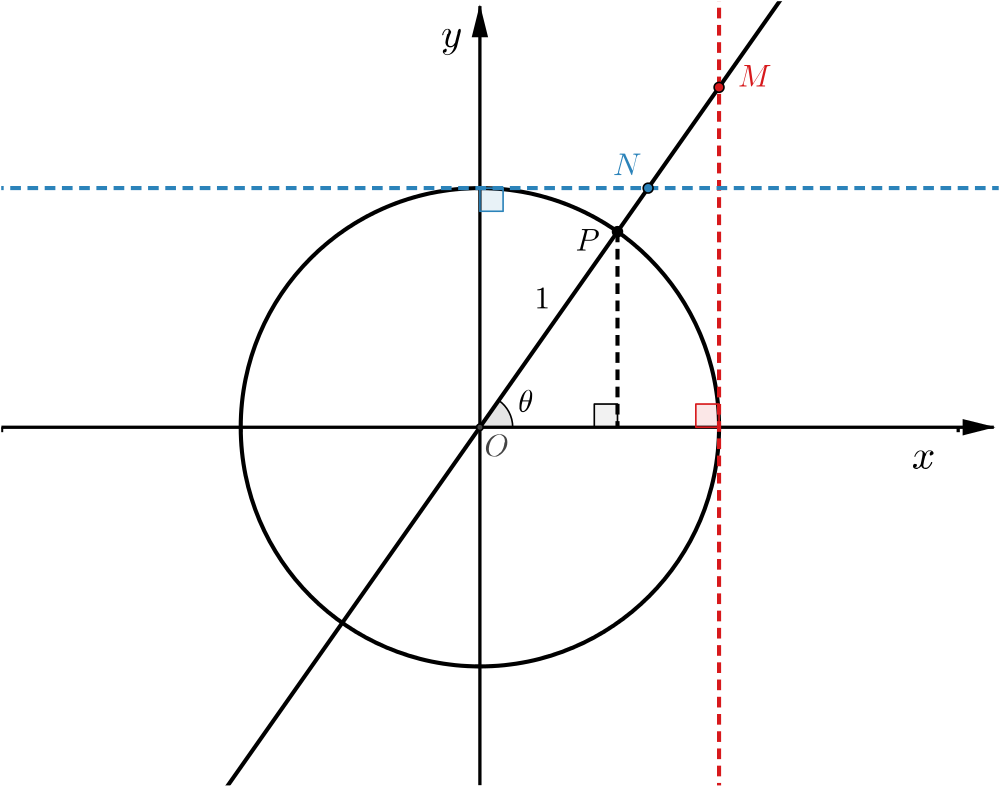
Using the functions from the triangles problem, work out the coordinates of points \(P\), \(M\) and \(N.\)
As \(\theta\) varies, how will \(M\) and \(N\) move? What happens when \(\theta\) isn’t acute?
- When will \(M\) and \(N\) be moving quickly?
- Do \(M\) and \(N\) always move smoothly?
- When will their \(x\)- or \(y\)-coordinates change sign?
In the next diagram, we have drawn the tangent to the circle at \(P\) and marked the points where the tangent at \(P\) meets the axes.
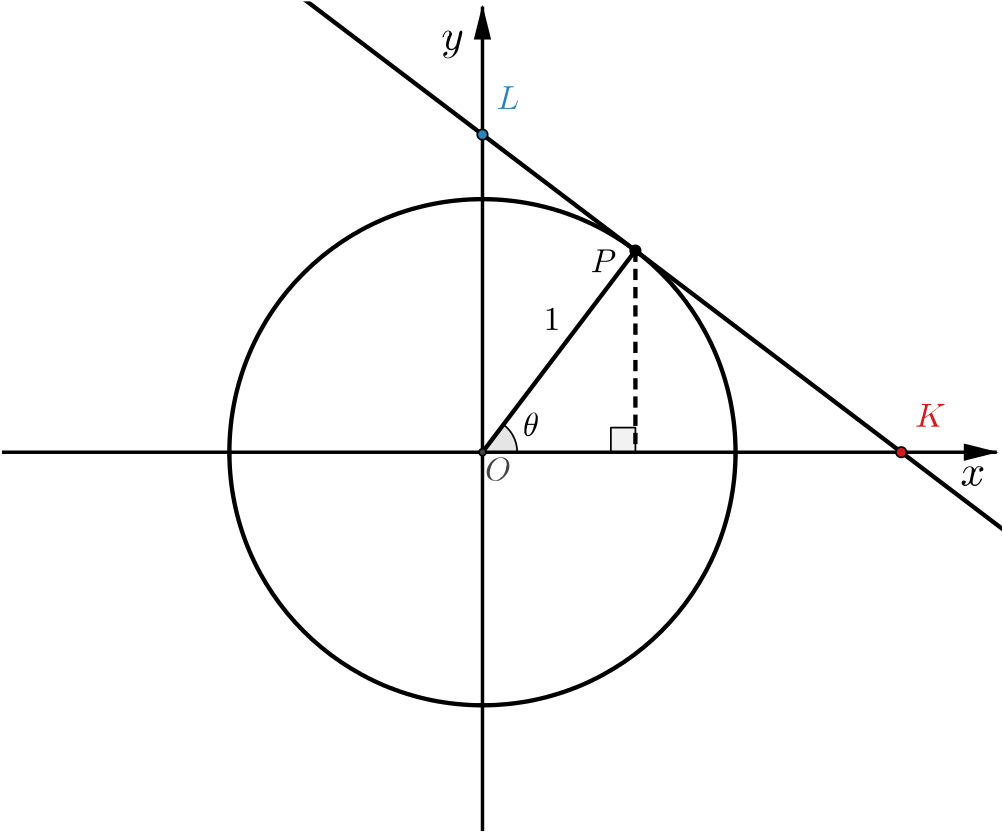
What are the coordinates of \(K\) and \(L\)? How will \(K\) and \(L\) move along the axes as \(\theta\) varies?

