Archimedes was the first person to determine the surface area of a sphere, which he wrote in a work called On the sphere and cylinder in the 3rd century BCE.
The fact that the area of a sphere is equal to the area of the cylinder surrounding the sphere led to the creation of a variety of area-preserving world maps, such as the Lambert Projection (1772). In general, these are known as cylindrical equal-area projections. In these maps, equal areas on the Earth’s surface correspond to equal areas on the map.
Here is a modern example of such a map:
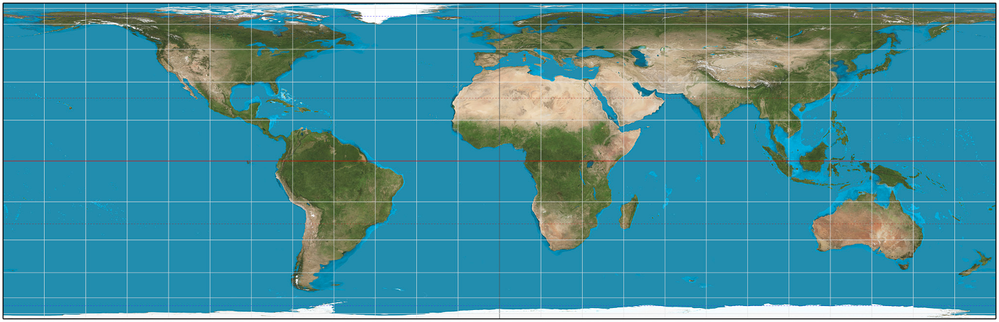
(Image taken from Wikimedia Commons, copyright Strebe 2011, licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license.)
What interesting things do you notice about the world when it is mapped in this way?

