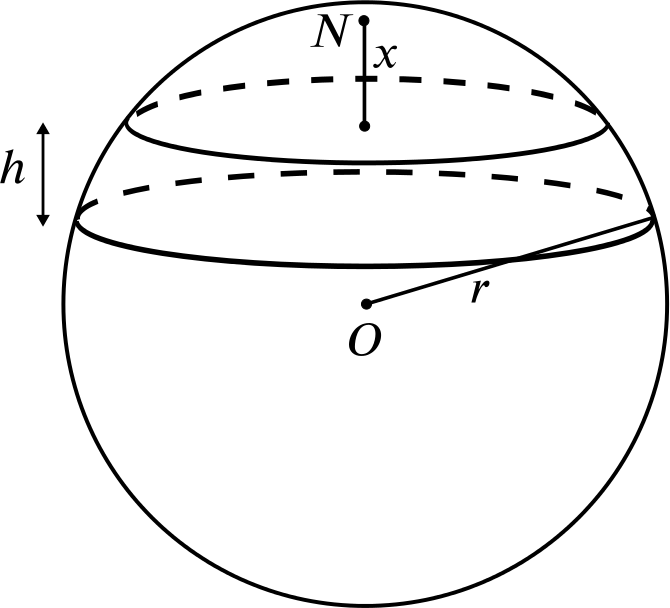
The sphere in the diagram has radius \(r\) and is cut by two parallel planes distance \(h\) apart.
One of these planes is at a distance \(x\) from the “north pole” of the sphere, as shown in the diagram.
What is the surface area of the part of the sphere lying between these two parallel planes?
The suggestion proposed considering special cases, so that’s what we’ll do.
One special case we could consider is when \(x=0\). If \(h=r\), then we have a hemisphere. You may have learnt that the surface area of a sphere is \(4\pi r^2\), so the answer in this case is \(2\pi r^2\). Likewise, we can consider the most extreme cases: when \(h=2r\), we get an area of \(4\pi r^2\) (the entire sphere), and when \(h=0\), we get zero area.
So if we do manage to get a general formula, we will be able to check it in these special cases.
Another possible idea when \(x=0\) is to consider what happens when \(h\) is very small. In this case, the surface area looks a lot like a circle, but the radius of the circle does not seem particularly easy to work out, so maybe we’ll leave this one for a moment. (There are things we can do to approximate the radius using more advanced techniques, but they are currently beyond us.)
Another thing we could consider is the situation where \(h\) is very small. Then the part of the sphere between the planes looks very much like the frustum of a cone, and we know how to find the (surface) area of such a shape – see Cones.
If we recall our answer from that problem, we find the formulae for the surface area \[\pi(R+r)s=\frac{\pi(R+r)h}{\cos\theta}= \frac{\pi(R^2-r^2)}{\sin\theta}.\] Here, \(R\) is the radius of the base of the frustum, \(r\) is the radius of the top, \(h\) is the perpendicular height, \(s\) is the slant length and \(\theta\) is the angle the slant makes with the vertical.
Confusingly, that problem also used an \(r\) (to mean the radius of the top of the frustum), but our problem uses \(r\) to mean the radius of the sphere. So we’re going to have to be very careful when using the formula here to avoid getting confused.
Let’s draw a thin slice of our sphere to see which of these values are easy to work out.

The perpendicular height of this frustum is just \(h\), the thickness of our slice.
The radii of both the base and top of this frustum are about \(r\cos\varphi\), as can be seen from the diagram; the difference between the two radii is tiny.
The slant length \(s\) is a little harder to work out, but the slant angle is easier to see from the diagram. Because the slant of the slice is perpendicular to the radius of the sphere meeting it, the slant is at an angle of \(\varphi\) to the vertical:

So now we have everything we need to work out the surface area of this frustum. We’ll use the formula \(\dfrac{\pi(R+r)h}{\cos\theta}\).
We don’t know \(s\), so we can’t use \(\pi(R+r)s\) directly. We also don’t know \(R\) and \(r\) accurately enough to be able to work out \(R^2-r^2\), so we can’t use the third formula.
Substituting in our values: both radii are \(r\cos\varphi\), the perpendicular height is \(h\) and the angle the slant makes with the vertical is \(\varphi\), so the area is \[\dfrac{\pi(r\cos\varphi+r\cos\varphi)h}{\cos\varphi}=2\pi rh.\]
This is a real surprise! The answer does not depend on \(\varphi\) (or equivalently, \(x\)) at all! And it is the same as the surface area of a cylinder also of radius \(r\) and height \(h\).
So when \(h\) is really small, the area of the strip of the sphere is about \(2\pi rh\). The smaller we make \(h\), the more accurate this estimate becomes, as the slice will look more and more like a frustum of a cone.
We are now in a position to solve the main problem. We have a section of the sphere with height \(h\). If we slice it into \(n\) slices, each with height \(h/n\), then the surface area of each one will be about \(2\pi rh/n\), so in total, the area will be about \[n\times 2\pi rh/n=2\pi rh.\]
If we take more slices, our frustum-of-a-cone-shaped slices will become closer and closer to the actual shape of the sphere, so our approximation will become more and more accurate.
So the area of the section of the sphere really is \(2\pi rh\). This is the same as the surface area of a cylinder of the same radius as the sphere and height \(h\).
We can check this with our special cases: if \(h=r\), then this formula gives \(2\pi r^2\), and if \(h=2r\), we get \(4\pi r^2\).

