What about the two-dimensional analogue of this problem? That is, we take the original problem and change every “sphere” into “circle”, every “plane” into “line”, and ask about lengths instead of areas, as follows:
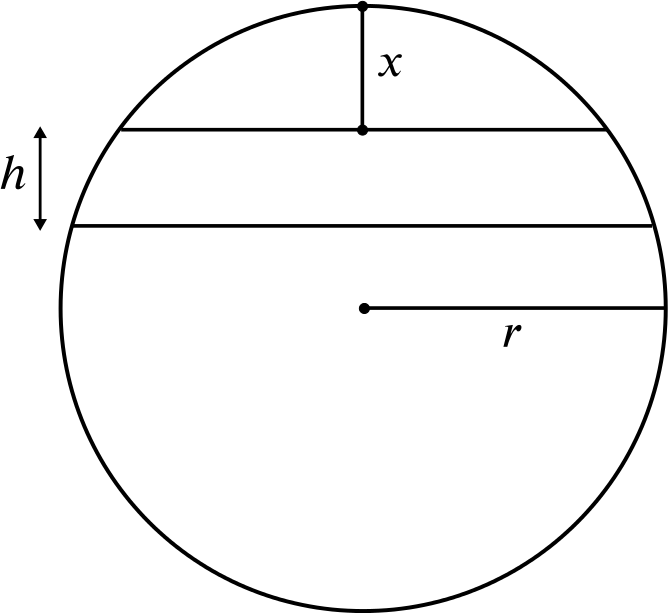
The circle in the diagram has radius \(r\) and is cut by two parallel lines distance \(h\) apart.
One of these lines is at a distance \(x\) from the “top” of the circle, as shown.
What is the length of the parts of the circle lying between these two parallel lines?
How does this question compare to and contrast with the original sphere problem?

