Throughout, \(A\), \(B\) and \(C\) are the angles of a triangle.
For each of the following, decide whether it is an identity (true for all triangles) or an equation (there is a triangle for which it is not true).
If it is an identity, true for all triangles, then you should prove it (perhaps using trigonometric identities that you already know).
If it is an equation, then at the very least you should give an example of a triangle for which it is not true. You could also try to solve the equation (that is, find all triangles for which it is true).
\(\sin(\frac{\pi}{2} - A) = \cos A\)
We have to decide whether to show that this is an identity or to solve the equation. To help us decide, we could try some particular values. We should choose values that will lead to sines and cosines that we can compute easily, but not such special cases that they run the risk of misleading us.
If we try \(A = \frac{\pi}{3}\), the left-hand side becomes \(\sin(\frac{\pi}{6}) = \frac{1}{2}\) and the right-hand side is \(\cos(\frac{\pi}{3}) = \frac{1}{2}\). So the equation holds in this case.
Doing that example might have reminded us of a useful diagram.
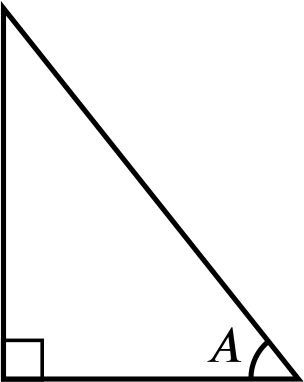
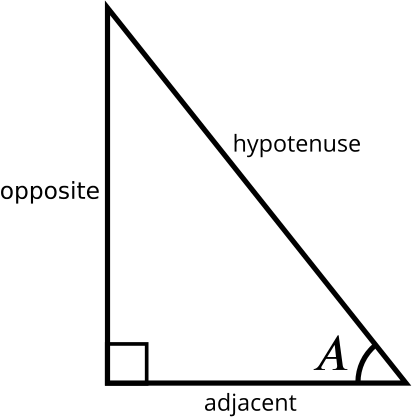
We define \(\cos A\) to be the adjacent over the hypotenuse. But we can see that this is precisely the sine of the other angle that isn’t a right angle, which is \(\frac{\pi}{2} - A\). So we have \(\sin(\frac{\pi}{2} - A) = \cos A\).
Alternatively we could think about the connection between the graphs of sine and cosine.
\(\sec^2 A - \tan^2 A = 1\)
One of our key trigonometric identities is that \(\sin^2 A + \cos^2 A = 1\) for all angles \(A\) (not just those in a triangle). We might recognise the equation in the question as a common variant.
We know the familiar identity \[\sin^2 A + \cos^2 A = 1.\]
Dividing through by \(\cos^2 A\) gives \[\tan^2 A + 1 = \sec^2 A,\] and we can rearrange this to \[\sec^2 A - \tan^2 A = 1.\]
We should be slightly more careful, however: we cannot divide by \(\cos^2 A\) if it is zero, and this could happen when \(A\) is an angle of a triangle.
The equation holds for all values of \(A\) in the range except \(A = \frac{\pi}{2}\) (when the left-hand side is undefined).
\(\tan(A + B) = - \tan C\)
We might try some values here.
We might also remember that \(A\), \(B\) and \(C\) are the angles of a triangle, so \(A + B + C = \pi\).
We have \[\tan(A + B) = \tan(\pi - C)\] whenever both sides are defined (that is, whenever \(C\) is not a right angle).
It may be convenient to refer to a sketch of \(y = \tan x\).
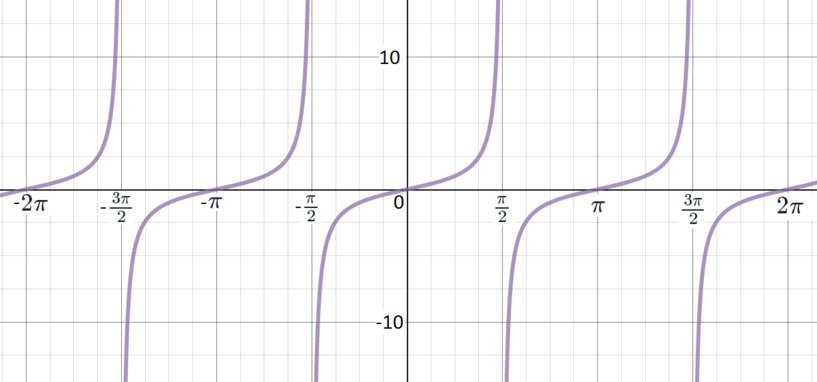
We know that tan is a periodic function, with period \(\pi\), so \[\tan(\pi - C) = \tan(-C).\] Since tan is an odd function, we have \[\tan(-C) = -\tan C.\]
Putting this together, we find that \[\tan(A + B) = - \tan C\] for all triangles where \(C\) is not a right angle.
\(\sin^2 A - \cos^2 B = 1\)
Let’s try some values to try to get a feel for whether this is an equation or an identity.
If \(A = B = \frac{\pi}{4}\) (note that these are indeed possible angles in a triangle), then \[\sin^2 A - \cos^2 B = 0.\]
So it is not an identity; we should try to find the values for which the equation does hold.
One difficulty about the given equation is that the two terms on the left differ in two ways: sine versus cosine, and \(A\) versus \(B\). We could do something about that by replacing the \(1\) on the right-hand side by \(\sin^2 A + \cos^2 A\).
If \[\sin^2 A - \cos^2 B = 1,\] then \[\sin^2 A - \cos^2 B = \sin^2 A + \cos^2 A,\] so \[-\cos^2 B = \cos^2 A.\] The right-hand side is always at least zero, whereas the left-hand side is always at most zero. The only way they can be the same is if they are both zero.
So if \(A\) and \(B\) are part of a triangle that satisfies the equation, then \(\cos A = \cos B = 0\).
This means that \(A = B = \frac{\pi}{2}\), and this is not possible in a triangle (at least in a non-degenerate triangle).
So there are no solutions to the equation.
\(\sin(\pi - A) = \sin B\)
It’s reasonably clear that this cannot be an identity; it will be easy to think of examples of angles for which it does not hold, because there’s so much flexibility about choosing \(A\) on the left-hand side and \(B\) on the right-hand side. So we should try to solve the equation.
We know that \(\sin(\pi - A) = \sin A\), so we are looking to solve \[\sin A = \sin B.\] This has the obvious solutions \(A = B\), but also the slightly less obvious solutions \(B = \pi - A\). The latter cannot happen for a (non-degenerate) triangle, so we see that a triangle satisfies the equation if and only if it is isosceles with \(A = B\).
\(\sin^2 A - 3\cos A = \cosec^2 C - \cot^2 C\)
This is rather complicated. How might we simplify it? We might recognise the right-hand side as something that we could simplify.
We have \[\sin^2 C + \cos^2 C = 1,\] so dividing through by \(\sin^2 C\) gives \[1 + \cot^2 C = \cosec^2 C,\] and so \[\cosec^2 C - \cot^2 C = 1.\] This holds as long as \(\sin C\) is not zero, and this will be true when \(C\) is an angle of a (non-degenerate) triangle.
So the equation we’re given is \[\sin^2 A - 3 \cos A = 1.\]
We can make this more manageable by replacing \(\sin^2 A\) with something involving \(\cos A\).
This is equivalent to \[(1 - \cos^2 A) - 3\cos A = 1,\] that is, \[\cos^2 A + 3\cos A = 0.\] Factorising, this becomes \[\cos A (\cos A + 3) = 0,\] so \(\cos A = 0\) or \(\cos A = -3\).
The latter option is not possible, so if we have a solution then we must have \(\cos A = 0\) and so \(A = \frac{\pi}{2}\).
We see that a triangle with angles \(A\), \(B\) and \(C\) satisfies the equation if and only if it is right-angled with a right angle at \(A\).
Notice that although \(C\) appears in the equation we’re given, whether or not there is a solution does not depend on \(C\).

